JJF1070-2005《定量包裝商品淨含量計量檢驗規則》理解與實施

第四講  定量包裝商品淨含量的（de）計量檢驗

江蘇省質量技術監督局　黃耀文

　　《規則》第五章和（hé）第六章分別闡述了（le）對定量包裝商品淨（jìng）含量的計量檢驗（yàn）和檢驗（yàn）結（jié）果的評定和報告的要求。這兩方麵的要（yào）求是在（zài）對（duì）定量包裝商品淨含量計量檢驗中必須嚴格遵循的（de）基本（běn）要求，也是全麵理解和正確貫徹實施《規則》的（de）核心。    

　　一、計量檢（jiǎn）驗的總體要求

　　在（zài）《規則》第（dì）五章第一節《總（zǒng）則》中，對定量包裝商品淨含量計量檢驗明確了兩個原則性的要求，一是計量檢驗應采用（yòng）的方法；二是在檢驗時應考慮的因（yīn）素。

　　1.計量檢驗應（yīng）采用的方法
　　(1)《規則》的要求
　　在《規則》5.1.1條款中規（guī）定:“對定量包裝商品淨含量實（shí）施計量監督檢驗應按（àn）照本規則的要求和程序進行。本規則的附錄規定（dìng）了以不同（tóng）方式標注淨含（hán）量的定量包裝商品應采用的檢驗方法。本規則沒有規定檢（jiǎn）驗方法的定量包裝商品按國際（jì）標準（zhǔn）、國家（jiā）標準或者由國家質（zhì）量監督檢驗檢疫總局規定的方法（fǎ）執行。”

　　(2)要求的（de）理解與實施
　　①檢驗方法是影響檢驗結果的重要因素。為保證檢驗結果的統一性（xìng）、有效性和準確性，在《規則》附錄中（zhōng）給出（chū）了常見商（shāng）品的淨含量計量檢驗方法，供（gòng）我們在對商品實施檢驗時選用，其中包括，隨機抽樣方法、除（chú）去皮重的方（fāng）法、以質量(重量)標注淨含量商品的計量檢驗（yàn）方法；以體積標注淨含量商品的計量檢（jiǎn）驗方法；以長度標注淨含量商品的計量（liàng）檢驗方法；以麵（miàn）積標注淨含量商品的計量檢驗方法（fǎ）；以（yǐ）計數（shù）標注淨含量商品的計量檢驗方法(對上述檢驗方法的具體介紹可見第五、六講)。
　　對於個別特殊的定量包裝商品，如果附錄給出的檢驗方（fāng）法不（bú）適用，可按國際標準、國家標準或（huò）國家計量行政（zhèng）部門規定的方法執行。
　　②對具體的定量包裝商品淨含量實施計量檢驗時，應根據被檢（jiǎn）商品（pǐn）淨含量標注單位和商品特性，選擇附錄中給出的適當（dāng）方法。如檢驗以體積單位標注淨含量的洗（xǐ）發液，首先可確定應用附錄D《以體積單位標注淨含量（liàng）商品的計量檢驗方法》，然後根據洗發液（yè）流動（dòng）性（xìng）不好的特點，選擇相對密度法進行計量檢驗。

　　2.計量檢驗時應考慮的因素
　　(1)《規則》的（de）要求
　　在《規則》5.1.2條款中規定:“在檢驗定量包裝商品淨含（hán）量時，應當充分考慮水分變（biàn）化等因素對定量包裝商品淨含量產生的影響。
　　對因水分變化等因素導致淨含量變化較大（dà）的定量包裝商品，如麵粉、肥（féi）皂等商品，生產者應當采取措施保證在規定條（tiáo）件下商品淨含量的準確性。質量技術監督部門對此類定量包裝商品的計量監督檢查（chá）原則上應在（zài）生產現場進行。”

　　(2)要求的（de）理解（jiě）與實施
　　①眾所周知，有一部分定量包裝商品(如麵粉、肥皂等)由於商品（pǐn）自身的特點，根（gēn）據產品標準，允許含有一定比例的水分（fèn）。而（ér）水分又極（jí）易（yì）受環境條（tiáo）件和包裝材料的影（yǐng）響而發生變化（huà）。天氣（qì）幹燥易揮發，商品淨含量減少；天氣潮濕則商品水分增大，商品淨含量增加。因此，容易造成因水分變化導致商（shāng）品（pǐn）淨含量的增減，在生產者和消費者之間引發計量糾紛。
　　②對於此類（lèi）商品的（de）計量檢驗，作為質量技術監督部門，為了確保對定量包裝商品計量監督（dū）的科學性和準確性，在進行監督檢查，特別是檢驗淨含（hán）量是否符合要求時，一定要給予充分考慮，要科學合理地選擇（zé）檢查對象和檢查場所，特別是檢查場所。對其實施的計量監督檢查，原則上應當在生產企（qǐ）業進行。
　　③為了最大限度地避免這些糾紛的產生，本條款同（tóng）時對（duì）定（dìng）量包裝商品的生產者作出了規定（dìng），要（yào）求生產含水分比率較大的定量包裝商品的生產者采（cǎi）取措施，保證在規（guī）定條件（jiàn）下商（shāng）品（pǐn）淨含量的（de）準確。其含義是，生產者（zhě）應當明示所（suǒ）生產的商品在什麽樣的環境條件下，其含水量及淨含量究竟是多少，以便為檢驗提供依據。不能商品淨含量發生短缺就將其原因歸到水分揮發上。在商品生產工藝過程中（zhōng）添加一定比（bǐ）例的水分以及在商品（pǐn）儲存和運輸過程中水分的揮發問題是不可避免的，但重要的是，生產者要（yào）采取（qǔ）必要的措（cuò）施，不斷改進生產工藝，提高包裝水平，以應對並不斷地解決這些問題。    

　　二、計量（liàng）檢驗的測量不（bú）確定度（dù）要求

　　在《規則》第五章第二節《測量不確定度》中，對計（jì）量檢驗結果的測量（liàng）不確定度作出（chū）了明確的要（yào）求，該要求與原《規則》的要求有著重要的區別。
　　1.《規則》的要求
　　在《規則》5.2條款（kuǎn）中規定“定量包裝商品淨含量計量檢（jiǎn）驗結果的擴展不確定度不應超過0.2T，其置信水平為95%。其中（zhōng）置信（xìn）水平與測量儀器和檢驗方法有關。影響不（bú）確定度的因（yīn）素包括測（cè）量儀器的最大允（yǔn）許（xǔ）誤差和重複性等計量特性、包裝材料的變化，以及由於在液體中不同的固體數量或者（zhě）溫度的變化引起的密度波動（dòng）等。”

　　2.要求的理解與實施
　　①為（wéi）了保證檢驗結果的準確可靠，《規則（zé）》對（duì）計量檢驗的準確度提出了新的更高的要求。原《規則》僅僅對計量器具的選擇作出了規定，要求“計（jì）量器具的最大允許（xǔ）誤（wù）差應小於（yú）或等於被檢驗商品最大（dà）允許負偏差絕對值的三分之一”，而對檢驗（yàn）結果的不（bú）確（què）定度沒有提出任（rèn）何要求。而《規則》明確規定了“定量包裝商品淨含量計量檢驗結果的擴展不確定度不應超（chāo）過（guò）0.2T，其置信（xìn）水（shuǐ）平為95%。”
　　②擴展不確（què）定度是由合成標準不確定度的倍數表示的測量不確定度，通常用符號U表（biǎo）示。它是將合成標準不確定（dìng）度擴展了k倍得到的（de），即U=k，k值一般為2，有（yǒu）時為3，取決於被測量的重要性、效應和（hé）風險。
　　擴展不確定度是測量結果的取值區間的半（bàn）寬度，可（kě）期望該（gāi）區間包含了被測（cè）量之值分布的大（dà）部分。而測量結果的取值區（qū）間在被（bèi）測量值概（gài）率（lǜ）分布中所包含的（de）百分數（shù），被稱為（wéi）該區間的置信概率、置信水準或置信水平（píng），用符號p表示，擴展不確定度用符號U表示，它給出的區間能包含被測量（liàng）可能值的大部分(如95%或99%等)。
　　③承（chéng）擔定量包裝商品（pǐn）淨（jìng）含量（liàng）計量檢（jiǎn）驗的計量檢定機構（gòu），必須按此要求對所開展項目的（de）測量不確定度進行評定，並確保滿（mǎn）足《規則》所規定的（de）要求。在對檢驗結果（guǒ）進行（háng）測量不確定度評（píng）定時，應充（chōng）分考慮各種影響不確定度的因素（sù），包括檢驗用測量設備的（de）計量特性，被檢商（shāng）品包（bāo）裝材料的變化，以及（jí）被檢商品因自身（shēn）特（tè）性或環境條（tiáo）件變化所引起的淨含量的變化等。根據（jù）《規則》的要求，用於計量檢驗的（de）測量（liàng）設備的最（zuì）大允許誤差應小於0.2T。    

[page_break]

　　三、計量檢驗（yàn）的統計與控製準則

　　在（zài）《規則》第五章第三節《統計與（yǔ）控製準則（zé）》中，根據統計抽樣檢驗的（de）原理，對計量檢驗抽樣方案產生的背景和存在的兩類風險作了具體的說明，以便使計量檢（jiǎn）驗（yàn）人員能夠從理（lǐ）論和（hé）實際的（de）結合上理解和掌握計量檢驗方案。

　　1.計量檢驗的控製準則
　　(1)《規則》的要求
　　在《規則》的5.3.1條款“控製準則”中規定:
　　“接受或拒絕一個檢（jiǎn）驗批的檢驗應（yīng）考慮以下3個因素:
　　①定量包裝商品的平均實際含量的誤差；
　　②單件定量包裝商品實（shí）際含量小於標注（zhù）淨含量減去允許短缺量T的商品占檢（jiǎn）驗批的百分比小於2.5%；
　　③檢驗批中，沒有一件單件定（dìng）量包裝商品的實際含量小於標注淨含（hán）量減去兩倍的（de）允許短缺（quē）量。”

　　(2)對（duì）要求的理解
　　①對定量包裝商品淨含量實施的計量檢驗是統計抽樣（yàng）檢驗。統計抽樣（yàng）檢驗是建立在（zài）概率論與數理統計（jì）、管理學和經濟學等理論（lùn）基礎上的一種檢驗方法。本條款規定的計（jì）量（liàng）檢（jiǎn）驗的控製準則（zé），是《規則》製定計量檢驗抽樣方案的依據。控製準則包括兩類因素，一個是關於定量包裝商品的平均實際含量的控製因素，另一個是關於單（dān）件定（dìng）量包裝商品實際含量的控製因素，它們反映了（le）定量包裝（zhuāng）商品淨含量的兩種不同的質量特（tè）征。
　　②按照單位產品的質量特征，統（tǒng）計抽樣檢驗可分為計數抽樣檢驗（yàn）和計量抽樣（yàng）檢驗兩種。計數抽樣檢驗:按照規定的質量標準，把單位產品簡單地劃分為合格品或不（bú）合格品（pǐn），或者隻計算缺陷數，然後根據樣本的檢驗結果對檢驗批進行（háng）評定的一種檢查方法。計數抽樣檢驗（yàn）隻把樣（yàng）本中的每個單位產品簡單地劃分為合格品或不合格（gé）品，根據樣本中（zhōng）不合格品的個數，按預先規定的判斷準則來決（jué）定該檢驗批是否合格。計量抽樣檢驗:對單位產品的質量特征，必須用某種與之對應的（de）連續量(例如時間（jiān）、質量（liàng）、長（zhǎng）度、麵積等)實際測量，然後根（gēn）據（jù）統計計（jì）算結果(例如平均（jun1）值、標準差（chà）或其他統計量等)是否符合規定的接收評定值或接收準則，對檢驗批（pī）進（jìn）行評定。計量抽樣檢驗需要測定樣本中每個單位產品的某一定量指標(如尺寸、質量、長度、麵積（jī）等)，然後計算某個統計量的值，按預先規定（dìng）的判斷準則來決定該檢驗（yàn）批（pī）是否合格。
　　在《規則》規定的監（jiān）督抽（chōu）樣檢驗方法中，對於（yú）檢驗批的單件（jiàn）定（dìng）量包裝商品淨含量的檢驗，即因素②和（hé）③，使用的是計數抽樣檢驗的（de）方法；對於（yú）檢驗批平均實際含量的檢驗，即因素①，使用的是計量抽樣（yàng）的方法。
　　③計數抽樣檢驗方案是一組（zǔ）特定的規則，用於對批進行檢驗、判定。它包括樣（yàng）本量n和判定數組Ac和（hé）Re。Ac是對批（pī）作出接收判定時，樣本中發現的不合格品(或不合格數)的上限值，隻要樣本中發現的不合格品(或不合（hé）格數)等於或小於Ac，就可以（yǐ）接收該批（pī）。Re是對批作（zuò）出不接收判（pàn）定時，樣本中發現的不合格品(或不合格數)的下（xià）限值，即當樣本中（zhōng）發現的不合格品(或不合格數)等於或大於（yú）Re時，則可判定不接收。
　　上述檢驗方案中的n，是由檢驗方案的檢（jiǎn）驗水平確定的。檢驗水平規定了批量與樣本量之間的關係。根據國（guó）家（jiā）標準GB/T2828.1/ISO2859-1:2003《計數抽樣檢（jiǎn）驗程序 第一部分:按接收質量限(AQL)檢索的逐批檢驗抽樣計劃》的表的設（shè）計，使批量較大時的樣本量在一般情況下要大於批量較小（xiǎo）時的樣本量。但是其比例並不會變大，反而是大批量時的樣本量比例要小於小批量時的比例。在該標準中，給出了3個一般檢驗水平，分別是水平Ⅰ、Ⅱ、Ⅲ，還（hái）有（yǒu）4個特殊檢驗水平，分別是S-1、S-2、S-3、S-4。數碼越大，等級越高；一般檢驗水平高於特殊檢驗水平；水平Ⅰ的樣（yàng）本量不（bú）到水平Ⅱ的樣本量的一（yī）半，水平Ⅲ的樣本量大約是水平（píng）Ⅱ的1.5倍。常用的是一般水平，並且水平Ⅱ最為常用，除非專門指定用其他的水平。在《規則》中（zhōng）檢驗方案采用的檢驗水平是一般水平中的水平Ⅱ。
　　上述（shù）檢驗方案中的Ac和Re，是由（yóu）檢驗方案的接收質（zhì）量限確定的。接收質量限，是當一個連續係（xì）列批被提交驗收抽樣時，可允許的最差過程平均質量水平，以符號AQL表示。在GB/T2828.1/ISO2859-1:2003標（biāo）準（zhǔn）中，接收質量限（xiàn）被作（zuò）為一個檢索工具。使用這些按AQL檢索（suǒ）的抽樣方案，來自質量等於或好於AQL的過程的檢驗批，其大部分將被接收。AQL是可以接（jiē）收和不可以接收的過程平均之間（jiān）的界限值。在規定AQL時，必須知道AQL表明了生產中所要求的（de）質量。生產方應按要（yào）求生產，使提交（jiāo）批的平均質量水平優於AQL。一方麵（miàn），這種質量必須是合理的（de），可以（yǐ）達到的；另一方麵，該質量從使用方的觀點來看也必須是合理的。這常常意味著在使用方所喜歡的質量和生產方（fāng）所能提供的質量之間達（dá）成一個妥協。
　　在《規則》的抽樣（yàng）方案中規定，單件定量包裝商品實際含量小於標注淨含量減去允許短缺量T的商品占檢驗批的百分比小於2.5%，即接收質量限(AQL)為2.5%。

　　④計量抽樣檢驗的接收規則與計（jì）數抽樣檢驗的接收規則的（de）根本（běn）區別是，前者（zhě）是以（yǐ）樣（yàng）本中各單位產品的計（jì）量質量特性為依據，而後者則以樣（yàng）本中所含不合格品(不合格項或不合格數)為依據。與計數（shù）抽樣檢驗相比，計量（liàng）抽（chōu）樣檢驗（yàn）能夠提供更（gèng）多、更詳（xiáng）細的產品質量（liàng）信息（xī），當產品質量下降時，計量抽樣檢驗會更早地發出警告。計（jì）量抽（chōu）樣檢驗需要假定質量特性服從（cóng）某種分布規律，如正態分（fèn）布、指數分布等，並且僅適用（yòng）於單個質量特性。計（jì）量抽樣檢驗的統計原理是數理（lǐ）統計中的統計推斷。
　　統計（jì）分析（xī）的基（jī）本目的是（shì）從樣本推斷（duàn）總體分布。這種（zhǒng）從樣本出發推斷總體分布的過程稱為統計推斷。例如，通過部分產品的檢驗推斷全部產品的質量。由於樣本數據的取（qǔ）得是帶有隨機（jī）性的，因此，需要用數理統計的方法來進行推斷。
　　統計推斷是（shì）數理統計學的核心部分。統計推斷基本上可以分（fèn）為兩類:一是參數估計，二是假設檢驗(統計檢驗)。現分別簡要介（jiè）紹（shào）如下。參數估計包括參數的點估計和參數的區間估（gū）計。參數的點估計的優點是不（bú）需要知道（dào）被估計（jì）的參數值，計算簡單，能（néng）給人一個（gè）明確（què）而具體的數（shù）值。缺點是隻從總體中隨機抽取一個樣本，所得點估計值（zhí）不能恰當（dāng）代表所（suǒ）估計的總體參數，換言之，點估計沒有解決參數估計的準確度（dù）和可（kě）靠性問題（tí）。為了彌補這些不（bú）足，提出了（le）參數的區間估計。
　　點估計是用一個數(一個（gè）點)去估計未（wèi）知參數。而區間估計是用一個區間去估計未知（zhī）參數（shù），即把未知參數值估計在兩個界限值之間。比如說，用點估計（jì）說:“該批定量包裝商品的平均實際含量（liàng）是（shì）50.03克（kè）”；用區間估計說:“該批定量包裝（zhuāng）商品的平均（jun1）實際含量是50.03克左右”。可見，點估計（jì）說話未留餘地，區（qū）間（jiān）估計說話留有餘地（dì），50.03克左右已把可（kě）能出現的誤差考慮了，這樣更能夠使（shǐ）人相信估（gū）計結果（guǒ）。區間（jiān）估計的關鍵是“左右”兩個字。左多少右多（duō）少才能保證估計的準確性和（hé）可靠性呢？解決這個問題的思路（lù）是設計一個區間，以最大的可能性保證（zhèng）被估計參數（shù）落在（zài）這個區間（jiān）內，以最小可能性防止被（bèi）估（gū）計參數落到（dào）區間外。

[page_break]

　　具體做法:
　　一是給出置信區間（jiān）。置信（xìn）區間又稱為（wéi）隨機區間(是合理的取值範圍)，Q_L是下界（jiè）限，Q_U是上界限（xiàn），置信（xìn）區間表達了區間估計的準確性。
　　二是給出顯（xiǎn）著性水平α。顯著性水平(又稱為判斷（duàn）錯誤概率、風（fēng）險度)α，它是（shì）一個（gè）小概率，表達了（le）區間估計的不可靠概率。
　　三是給出置（zhì）信（xìn）度1-α。置（zhì）信度(又稱（chēng）為置信概率、置信水（shuǐ）平)1-α表達了（le）區間估計的可靠性，它是區（qū）間（jiān）估計的可（kě）靠概率，通常（cháng）取接近於1的值。

　　在統計（jì）學中，α通常取以下三個值:
　　顯著性水平  置信水（shuǐ）平(置（zhì）信度)
　　α=0.10  → 1-α=0.90=90%
　　α=0.05  → 1-α=0.95=95%
　　α=0.01  → 1-α=0.99=99%
　　在定量包裝商品抽樣檢（jiǎn）驗中常用的是α=0.05。
　　假設檢驗是抽（chōu）樣推斷中的一項重要內容。它是根據原資料作出一（yī）個總體指（zhǐ）標是否等於某一個數值（zhí），某一隨機變量是（shì）否服從某種概率分布的假設，然後利用樣本資料采用（yòng）一定的統（tǒng）計方法計算出有關檢驗（yàn）的（de）統計量，依（yī）據一定的概率原則，以較小的風險來判（pàn）斷估計數值與（yǔ）總體數值（zhí）(或者估計分布與實際分布)是否存（cún）在顯著差（chà）異，是否應當接受原假設選擇的一種檢（jiǎn）驗方法。
　　用樣（yàng）本指標估計總體指標，其結論有的完全可靠，有的隻是一定程度（dù）的可靠，需要加以進一步的（de）檢驗和證實。通過檢驗，對樣本指標與假設的總體指標之間是否（fǒu）存在差別作出判斷，是否接受原假設（shè）。這（zhè）裏必須明確，進行檢驗的目的不是懷疑樣本指標本身是否計算正確，而是（shì）為了分析樣本指標和總體指（zhǐ）標（biāo）之（zhī）間是否存在顯著差異。從這（zhè）個意義（yì）上，假設檢驗又稱為顯著性檢驗。
　　進行假設檢驗，先（xiān）要對假設進行陳（chén）述。通過下例加（jiā）以說明。
　　例（lì）如，某食品廠用自動包（bāo）裝機（jī）將食品定量包裝成袋，每（měi）袋的標準重量為100g，每天開工時需要先檢驗包裝機工（gōng）作是否正常。根據以往（wǎng）的經驗（yàn），每（měi）袋食品的重量X服從（cóng）正態分布(μ，σ²)，標準差σ=0.85g，某天開工後抽測了8袋（dài），其重量(單位:g)如下:
　　101.2，101.4，99.7，99.5，101.3，99.6，101.0，101.6
　　試問:該天包裝機工作是否正常？(假定該天的（de）σ不變)
　　解答:上（shàng）例提出的（de）問題是“該天包裝機工作是否正常”，不是包裝機包裝出來的（de）食品每袋都是100g才算工作正常。因為受（shòu）隨機誤差的影響，每袋（dài）食品的重（chóng）量X是（shì）一個隨機變量。包裝機的工作即使是正常的怎樣確定這個常數，也不是每袋食品都正好是100g，而隻是在100g左右擺動。所謂“工作正常”，用（yòng）數理統計的語言來表達就是該天包裝機所包裝的食品的重量X的數學（xué）期望μ等於100g。我們要根據所獲（huò）得的樣本值判斷μ=100，還是μ≠100。為此，我們提出兩個相互（hù）對立的假設:
　　H₀:μ=μ₀=100  H₁:μ≠100
　　現（xiàn）在要檢驗（yàn）的（de）假（jiǎ）設涉及μ。μ是正態分布總體的數學期望。樣本平均值（zhí）是μ的性質優良的估計（jì）。所以很自然地考慮到用這個統計量來（lái）進行判斷。如果H₀:μ=100為真，雖然由於隨機因素的影響（xiǎng），與100之間的差異（yì）是（shì）不可避免的，但是它（tā）們之間的差（chà）異不能太大。所以我（wǒ）們應該尋找一（yī）個適當的常數K，使得當│-100│≥K時拒絕H₀，認為包裝機工作不正常；當（dāng）│-100│<K時接收H₀，認為包（bāo）裝機工作正常。
　　 這樣，問題便轉化（huà）為怎樣確定（dìng）常數（shù）K。這就需要給出確定（dìng）K的原則。我們的做法是，常數K的確定要符合如下原則:

　　當假設（shè）H₀:μ=100為真時，{│-100│≥K}是（shì）個小（xiǎo）概率事件。
　　若把這個小的概率記為α，上麵這句（jù）話就可以寫成P{│-100│≥K/H₀為真}=α。這樣做的（de）根據是實際推斷原理，即“概率很小的事件在一次試驗中幾乎不可能發生的”，也稱為小概率原理。
    根據這個原理，如果H₀:μ=100為（wéi）真，由K的做法知{│-100│≥K}是個小概率事件，所以在一次觀察中樣本均值的觀察值X滿足│-100│≥K是幾乎不可能的（de）。如果在一次觀（guān）察中居（jū）然真（zhēn）的（de）出現了滿足│-100│≥K的，我們就有理由懷疑假設H₀的正確性，因而拒絕Ho；相反，若（ruò）觀（guān）察值滿足│-100│<K，則表明假設H₀與實際情況（kuàng）沒有矛盾，此時沒有理由拒絕H₀，因而接受H₀。
　　將小概率事件│-100│≥K用等價事件{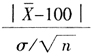≥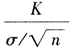}來表示，記K′=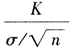，於是相應地確定K′即可。對於（yú）給定的（de）α
    由
　　p{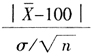≥K′/H₀為真}=α
　　知，我們要求的K′就是標準正（zhèng）態分布N(0，1)的1-α/2分位數 。於是可得到如下的檢驗規則:對於樣本均值的觀察值
　　若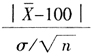≥，則（zé）拒絕H₀；
　　若（ruò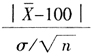）<，則接受H₀。
　　如（rú）果取α=0.05，由標準（zhǔn）正態分布表可以查到U_0.975=1.96。本題中n=9，σ=0.85，==100.53。經計算，
　　
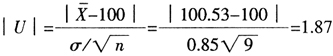
　　因為1.87<1.96=U_0.975，所以接受H₀，認為該天包裝機工作正常（cháng）。
　　通過這（zhè）個例（lì）子可總結出假設檢（jiǎn）驗的統計思想（xiǎng）如下:
　　設有某假設H₀需要檢驗(上述例子中為H₀:μ=100)，先假定該假設H₀是正確的，在此假（jiǎ）定之下構造一個具（jù）有已知分布的（de）統計量(上述例子中為U=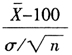)，並由此構造一個在H₀為真的條件下概率很小的事件。現（xiàn）進行一（yī）次試驗（yàn）(一次抽樣檢驗)，若小概率事件發生了（le），由實際推斷原理，使人懷（huái）疑H₀的正確性，從而拒絕H₀；若小概率事件不發生，就無法否定H₀的正確性，從而接受H₀。
　　在上述例子（zǐ）中提出的兩個（gè）相互（hù）對立的假設中，H₀稱為原假設(也稱為零假設（shè）)，H!稱為備擇假設(也稱為對（duì）立假設)。

　　綜上所述，假設檢驗的步驟可歸（guī）納如下:
　　(1)根據實際問題的要求，提出原假設H₀及備擇假設H!；
　　(2)給定顯著性水平α以及（jí）樣本（běn）容量n；
　　(3)確定檢驗統計量以及拒絕域的形式；
　　(4)按P{拒（jù）絕H₀|H₀為真}=α求出拒絕（jué）域；
　　(5)抽樣，根據樣本觀察（chá）值確定接受還是拒絕H₀。

　　2.統計抽樣檢驗的風險性
　　任何統計抽（chōu）樣檢驗都有（yǒu）一定的風險性（xìng），即使是（shì）100%檢驗也（yě）不能完全（quán）避免。抽（chōu）樣檢驗除了檢驗誤差之外（wài），還有來源於抽樣（yàng）本身的風（fēng）險，以至抽取的樣本不能真實地反映檢驗批的質量；其結果（guǒ）是在是否合格的問（wèn）題上（shàng）作出錯（cuò）誤的判斷，好的檢驗批被評定（dìng）為不合格；壞的檢驗批被評定（dìng）為合（hé）格（gé），樣本量越小這種風險越大。在抽樣檢驗中要完全避免風險，實際上是不大可能的。
　　(1)計數抽樣（yàng）檢驗的風險
　　在計數抽樣（yàng）檢驗中，即使檢驗批中實際存在不合格品百分數(每百單（dān）位產品不合格數)達（dá）到了規定的質量水平，也隻能以比較高的概率評定為合格，其結果是合（hé）格批（pī）被部分評定為不合格，這就給生產方（fāng）帶來了風險，稱為Ⅰ類風險(或“α”風險（xiǎn）)，也稱為生產方風險；而當檢驗批中實際存在的不合格品率或不合格數大於規定的質量水平，甚至達到一定的數值時，也隻能（néng）以較高或高概率評定為不合格，不能全部評定為不合格（gé），其（qí）結果是不合格批被部分（fèn）評定為合格，這就給使用（yòng）方（fāng）帶來了風險，稱為（wéi）Ⅱ類（lèi）風險(或“β”風險)，也稱為使用方風險。
　　所（suǒ）以，隻要采（cǎi）用抽樣檢驗，就有4種可能的判定(如表1所示（shì）)，其中必定要產生兩（liǎng）種錯誤的判定。即可能將接受批判定為不接受批，或者將不接受批判定為接受批。
    

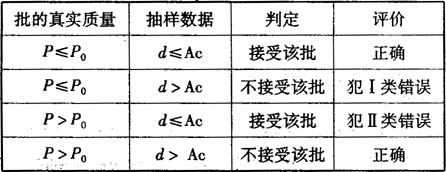
    表1  計數抽樣檢驗的評定風險

[page_break]

　　抽樣方案給生產方和使用方提供的保護，就（jiù）是減小這兩類風險（xiǎn）的程度。可通過計算對（duì）其進行調（diào）整。如果事先規定AQL質量批的不合格品百分數或每百單位產品不合格數以P₀表示，5至（zhì）10倍（bèi）AQL的劣質批的不（bú）合格品百分數或每百個單位產品不合格數以P_l表示，則可相（xiàng）應地（dì）計算出（chū）生產方風險和使用（yòng）方（fāng）風險。
　　α=1-Pa(P₀)
　　β=Pa(P)
　　(2)計量抽樣檢驗的風險
　　根據樣本（běn）資（zī）料對零假設作出接（jiē）收或拒絕的決定時，可能（néng）會出現以下4種情況（kuàng）:
　　①零假設為真，接受它；
　　②零假設為真，拒絕它；
　　③零假設為假，接受它；
　　④零假設為假，拒絕它。
　　上麵的4種情況，很顯然（rán），(2)與(3)是錯誤的決定。當然，人（rén）們都願意做出正確的決定，但事實上難以做到。因此，必須考慮錯誤的性質和犯錯誤的概率。我（wǒ）們把（bǎ）零（líng）假設為真時拒絕它，稱為第Ⅰ類錯（cuò）誤(或拒絕錯誤)；把零假設（shè）為假時接受它，稱為第Ⅱ類錯誤(或接受錯誤)。
　　　為了直觀起見，假設檢（jiǎn）驗出現的4種情況如表2所示。
    

    表2  計（jì）量抽樣檢驗評定的風險

　　第Ⅰ類型錯誤，記作α，即顯著性水平α；第Ⅱ類型錯誤，記作（zuò）β。α常用水平為0.05、0.01，是按所要求的精確度而事先規定的。它說明檢驗結果與（yǔ）擬定假（jiǎ）設是（shì）否有顯著性差距。如果有，就應拒絕擬定假設（shè）。但也（yě）有可能實際上符合擬定假設，隻是在抽樣（yàng）中偶然出現這（zhè）樣大的差距，那麽否定H₀就（jiù）犯了第Ⅰ類錯誤。從α的涵義（yì）可以看出，1-α是在擬定假設為真時的條件下，被接受（shòu）的概率（lǜ）。這是正確的判斷。
　　α與β不同，α是事先由決策者根據需要規定的，而（ér）β卻是（shì）計算出來的。根據理（lǐ）論計算表明，在樣本容量n固定（dìng）時，若（ruò）要減少犯第一類錯誤的可（kě）能，必（bì）將使犯第二類錯誤的可能（néng）性增加；而要減少犯第（dì）二類錯誤的可能，又將（jiāng）使犯第一（yī）類錯誤的可能（néng）性增加。
　　就檢驗的結果來說，拒（jù）絕原假設的（de）理由（yóu）是（shì）充分的，而接受原假設的理由則是不（bú）充分的。我們（men）之所以說“拒絕原假設的理由是充分的”，是（shì）因為對犯第一類錯誤的概率作了控（kòng）製(檢驗的水平α很（hěn）小)。這就使得（dé）在（zài）原假設為真時，錯誤地拒絕原假設的可能性很小(犯這種（zhǒng）錯誤的概率小於α)。因此，我們在拒絕原（yuán）假設時就有很大的把握。相反，我們之（zhī）所以說“接受原假設的理由是不（bú）充分的”，是因為沒有控製犯第二類錯誤的概率。這就（jiù）使在（zài）備擇假設為真時，錯誤地（dì）接受原假設的可能性並不小。從以（yǐ）上討（tǎo）論可以（yǐ）看出，在假設檢驗問題中原假設與備（bèi）擇假設的地（dì）位是不對（duì）等的。

　　(2)Ⅰ類風險檢驗的顯著水平
　　①定量包裝商品平均含量檢驗的Ⅰ類風險
　　在規則5.3.2.1條款（kuǎn）對定量包裝商品平均含量檢驗存在的Ⅰ類風險作了如下說明:“顯著水平(這類誤差的上限值)為0.005。檢驗決定在定量（liàng）包裝商品中商品量的平（píng）均值按照學生分布(t分布)具有99.5%的單邊顯著水平:
　　對於μ=Q_nα_μ≤0.5%
　　即:對於滿（mǎn）足μ=Q_n的正確定量包裝商品的檢驗批，其（qí）被拒絕的概率不超過0.5%。
　　這裏，μ為檢驗批的定量（liàng）包裝商品的商品量的平均值；α_μ為檢（jiǎn）驗批的定量包裝商品的商品量的平均值的Ⅰ類風險檢（jiǎn）驗的顯著（zhe）水平。”
　　②單件定量包裝商品淨含量檢驗的（de）I類風險
　　在規則5.3.2.2條款對單件定量包裝商品淨含量檢驗的Ⅰ類風險作（zuò）了如下說明:“短缺性定量包（bāo）裝商品百分比的檢驗有如下（xià）的顯著水平（píng）:對於p=2.5%，α_p≤0.5%
　　即（jí）:對於包含不超過2.5%短缺性定量包裝商品的檢驗批，其被拒絕的概率（lǜ）不超過5%。
　　這裏，p為檢驗批的單件（jiàn）定量包裝商品的實際含量的可（kě）接（jiē）收重量水平；α_p為檢驗批的（de）單件（jiàn）定量包裝（zhuāng）商品（pǐn）的實（shí）際含量的Ⅰ類風險檢（jiǎn）驗的顯著水（shuǐ）平。”

　　(3)Ⅱ類風險檢驗的顯著水（shuǐ）平
　　在規則5.3.3條款對檢驗方案（àn）的Ⅱ類風險檢（jiǎn）驗的顯著（zhe）水平作了如下說明:
    “通過檢驗至少90%的情況下，可發現如下特性的檢驗批:
　　a)檢驗批實際含（hán）量的平均（jun1）值小於(Q_n-0.74s)的情形。這裏s是檢（jiǎn）驗批定量包裝商品實際含量的樣品標準偏差；
　　b)檢驗批含有9%的短缺性定量包裝商品。”

　　3.定量包裝商品計量檢驗方（fāng）案分析
　　(1)對單件商品淨含量要求的檢驗方案分析
　　單件定量包（bāo）裝商品淨含量不符合《規則》規定的允許短缺量，可判定該商（shāng）品不合格。對（duì）單件定量包裝商品的淨含量要求是按照GB/T2828.1/ISO2859-1:2003《計數抽樣（yàng）檢驗程序 第一部分:按接（jiē）收質量限(AQL)檢（jiǎn）索的逐批檢（jiǎn）驗抽樣計劃》標準設計的計數抽樣檢驗方案。
　　該方案的檢驗（yàn）水平為正常檢查水平；質量合格水平(AQL)設定為2.5%，生產方風險(α)不大於5%，即對於P≤2.5%的檢驗批，通過（guò）檢驗（yàn）的概率不小於95%。對於檢驗批中（zhōng）含9%單件不合格定（dìng）量包裝商品的情況，通過檢驗至少有90%的概率能夠檢查出來，即（jí）使用（yòng）方（fāng）風險(β)不大於10%。
　　使用如圖1所示OC曲線圖，可以清晰地（dì）表（biǎo）示該方（fāng）案的各類風險。
    

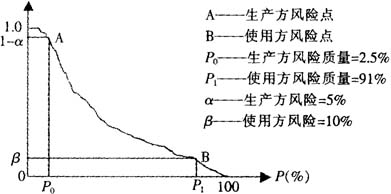
    圖1  單件商品淨含量檢（jiǎn）驗（yàn）OC曲線圖

　　(2)對平均淨含量要求的檢驗方（fāng）案分析
　　檢驗批定量（liàng）包（bāo）裝商品平均實際含（hán）量不（bú）符合《規（guī）則》規定的（de），可判定該檢驗批不符合。對檢驗（yàn）批商品（pǐn）平（píng）均含量的（de）抽樣檢驗是根據假（jiǎ）設檢（jiǎn）驗的理（lǐ）論，並按照GB/T4889-85/ISO2854:1976《數據的統計（jì）處理和解釋 正態分布均值和方差的估計與檢驗方法》標準設（shè）計的計量抽樣檢驗方案。
    該方案的顯著水平(這類誤差的上限值)為0.005。檢驗決定在定量包（bāo）裝商品中商品量的平均值按照學生分布(t分布)具（jù）有99.5%的單邊顯著水平（píng）:
　　對（duì）於μ=Q_n，α_μ≤0.5%
　　即:對於滿足μ=Q_n的正確定量包裝商品的檢驗批，其（qí）被拒絕的（de）概率不超過0.5%。
　　當（dāng）檢（jiǎn）驗批的實際含量的平均值小於（yú）(Q_n-0.74s)時，通過檢驗至少90%可以被檢出。這裏s是檢驗批（pī）定量包裝商品實際含量的樣品標準（zhǔn）偏差；
　　由此可見，檢驗批實際平均含量（liàng）的抽樣檢驗（yàn）方案對於生產（chǎn）方的（de）風險不超過0.5%；對於（yú）使用方（fāng）的風險不（bú）超過10%。  (未完（wán）待續)