計量培訓：測量不確定度表述講座
國家質量技術監督局  李（lǐ）慎安

　　7.1  合成標準不（bú）確定u_c的定義如何理解？
　　合（hé）成標（biāo）準不確（què）定度無例外地用標（biāo）準偏差給出（chū），其符號u以小寫正體c作為下角標；如給（gěi）出的為相（xiàng）對標準不確定度，則應另（lìng）加正體小（xiǎo）寫下角標rel，成為u_crel。按《JJF1001》定義為:當（dāng）測量結果是由若（ruò）幹個其他量的值求得時，按其他各（gè）量的方差和協（xié）方（fāng）差算得的標（biāo）準不確定（dìng）度。如各量彼此獨立，則協（xié）方差為零；如不為零(相（xiàng）關情況下)，則必須加進去。
　　上述定義（yì）可以理解為:當測量結果的標準不確定度由若幹標準不確（què）定度分量（liàng）構成時，按方和根(必要時加協方差)得到的標準不確（què）定度。有時它可以（yǐ）指某一（yī）台測量儀器，也可以（yǐ）指（zhǐ）一套測量係統或測量設（shè）備所複現的量值（zhí）。在（zài）某（mǒu）個量的不（bú）確定度隻以一個分量為主（zhǔ），其他（tā）分（fèn）量可忽略不計的情況下，顯然就無所謂合成標準不確定度了。

　　7.2  什麽是輸入量、輸出量？
　　在間接測量中（zhōng），被測量Y不能直接測量，而是（shì）通過若幹個別的（de）可以直接測量的量或是可以通過資（zī）料查出其值的量，按一定的函數關係得出（chū）:
　　Y=f(X₁，X₂，…，X_n)
　　其中X_i為輸入量，而把Y稱之為輸出量。
　　例如:被測量為一個立方體的體積V，通過其長l、寬b和（hé）高h三個量的測量結果，按函（hán）數關係V=l·b·h計算，則l，b，h為輸入量，V為輸出量（liàng）。

　　7.3  什麽叫作線性合成？
　　例如在測量誤差的合成計算中，其（qí）各個誤差分量，不論是（shì）隨機誤差分量還是係統誤差分量，當合成為測量誤差時，所有（yǒu）這些分量按代數和相加。這種合成的方法稱為線性合成。
　　不確定度的各個分量如（rú）彼此獨立，則恒用方和根的方式合（hé）成。但如果（guǒ）其中某兩個分量彼此強相關，且相關係數r=+1，則合成時是代數相（xiàng）加，即線性合成而非方和根合成。

　　7.4  什麽叫（jiào）靈敏（mǐn）係數？
　　當輸出量Y的估計值y與輸（shū）入量X_i的估計值x₁，x₂，…x_n之間有
　　y=f(x₁，x₂…，x_n)的函數關係時，在不確定度的傳播中，把偏導數，=c_i稱為靈敏係數，它（tā）定量地給出了輸入量（liàng）x_i，與輸出量y之間的相互變化關係之比（bǐ）值。它本身也是個量（liàng）值，有數值和量綱（gāng），往往（wǎng）其量綱並（bìng）非1，而是有測量單位的，這種情（qíng）況（kuàng）下不能（néng）將它按純數對待。
　　偏導數應該是（shì）在代入輸入（rù）量的估計值時作出評定，即在X_i=x_i時評定的。
　　
　　它描述了輸入（rù）估計（jì）值x_i的微小變化△x_i，引（yǐn）起y的變化(△y)_i=△x_i。如果這個變化（huà）是由估計值x_i的標準不（bú）確定度u(x_i)所引起，則y相應的變化為u(x_i)。因此，合（hé）成方差可以看作各項方（fāng）差之（zhī）和，而每（měi）一項代表了由每（měi）個輸（shū）入估計值（zhí）x_i相關聯之估計方差產生的（de）輸出估計值y的（de）估計方差。也就是（shì）:
　　式中:
　　c_i=，u_i(y)=|c_i|u_i(x_i)
　　以下給出幾種（zhǒng）比較簡單而又較常見的函數關係的靈敏係數:
　　(a)y=Ax₁+Bx₂
　　c₁=A；c₂=B
　　(b)y=1/x
　　c=-(1/x²)
　　(c)y=x₁/(x₁+x₂)
　　c₁=x₂/(x₁+x₂)²
　　c₂=-x₁/(x₁+x₂)²
　　(d)y=x/(1+x)
　　c=1/(1+x)²
　　(e)y=x₁x₂
　　c₁=x₂，c₁=x₁
　　(f)y=x²
　　c=2x
　　(g)y=x^1/2
　　c=1/2(2x^1/2)
　　
　　
　　以上A，B，a，b，k可以（yǐ）是（shì）負數或分數或等於1。
　　當用實驗方法求靈敏係數時，特別是（shì）在y與x_i之間不存（cún）在簡單（dān）函數關係時，可以通過將其餘輸入量保持不變，僅（jǐn）變化第i個x_i，設變化量為△x_i，由此而導致的y的變（biàn）化設為△y，則c_i=△y/△x_i。但也可通過函數關係計算出△y。
　　輸入量X_i的不確定度u(x_i)隻有在乘（chéng）了（le）相應（yīng）的靈敏係（xì）數c_i之後，才是輸出量Y的不確定度u(y)的一個分量u_i(y)。它們也才會（huì）有相同的量綱。

　　7.5  在線性函數關係中輸入量的相對標準不確定度u_rel(x_i)是否可以也按方和根合成為輸出量Y的相對標準（zhǔn）不確（què）定度u_rel(y)？
    在輸入量X₁，X₂，…，X_N彼此獨立（lì）的情況下，如果它們（men）與輸出量（liàng）Y的函（hán）數關係是線性的，例如最簡的一種情況:
    Y=X₁+X₂
若（ruò）已知u_rel(x₁)與u_rel(x₂)，是不能按方和根計算Y的相對標準不確定度u_rel(y)的（de）。例如:由兩個500g的砝（fǎ）碼相（xiàng）加，組成為輸出量1000g。每個（gè）500g砝碼的標準不確定度u(x₁)=u(x₂)=0.5g，則這輸出量1000g的不確定度實際上u(y)===0.71g。對1000g來（lái）說，其相對標（biāo）準不確定度應為u_rel(y)=0.71g/1000g≈0.7×10^-3。但如果用相對不確定度來合成，u_rel(x₁)=u_rel(x₂)=0.5g/500g=1×10^-3，它們未合成前已大於u_rel(y)。顯然是不合理的。
    有些情況下，例如在化學分析中，在給定濃度下的某些不確定度的分量，這些（xiē）分量的（de）相對標準不確定度均是除以（yǐ）某個相同的分母，而輸出量的相對標準不確定度也是這同一個分母，這時是可以采用方和根來合成相（xiàng）對標準（zhǔn）不確定度（dù）的。
    必須注意，盡管相對標準不確定度u_rel(x_i)都無（wú）例（lì）外地是無量綱量，它們都用純數（shù）給（gěi）出，但是這些純數並不都是（shì）無條（tiáo）件地可（kě）以相對減或（huò）是（shì）進行（háng）方和根運算的。因為這些數都是量值，而且往往（wǎng）是不同定（dìng）義的量值。
    也往往在這種相互獨（dú）立的（de）線性函數中，輸入量X₁與X₂按B類方法評定時，一開始就是（shì）給出的相對標準（zhǔn）不確定度u_rel(x₁)和u_rel(x₂)，例如通過測量儀器引用誤差評定的結果。那（nà）麽（me），由於分母不同(輸（shū）出量與輸入量)，也是不能采用方和根（gēn）得出輸出量的（de）相對合成標準不確定度u_crel(y)的。在這種情（qíng）況下，必（bì）須先把u_rel(x₁)與u_rel(x₂)算成標準不確定度u(x₁)與u(x₂)後再合成為u_c(y)；如這（zhè）時要求給出u_crel(y)，即可將u_c(y)除以y。這是當前極易被忽略的問（wèn）題之（zhī）一。
    7.6  當輸入量X_i與輸出量Y之間的函數關係（xì）為Y=f(X₁，X₂，…，X_N)=……時，是否也應按（àn）先算出靈敏係數c_i通（tōng）過=[c_iu(x_i)]²=(y)合成？
    可以這樣合成，但不一定（dìng）要如此複雜。采用這種方法需要麻煩的偏導數。更為簡單的辦法（fǎ）是（shì）采用輸入量的相對標準不確定度u_rel(x_i)=u(x_i)/x_i>乘以其相應的x_i的指（zhǐ）數p_i，即p_iu(x_i)/x_i，進行簡單的平方和得到輸出量Y的相對合成方差，即（jí）
    

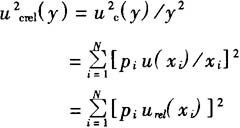
如果我們要求得到u_c(y)而不是u_-crel(y)，則可（kě）將得到的u_crel(y)乘以y即可。這是一（yī）種完全等效的（de）計算方法。
    例如通過物體質量m與其運動速度（dù）v的測量，求該物體（tǐ）的動能E_k。它們之間的函數關係式(稱測量模型)是:
    E_k=(1/2)mv²
    設輸入量m的標準不確定度為u(m)=lg，而m的最佳估（gū）計為1kg，速度v的（de）量佳估計為100m/s，其標準不確定度（dù）u(v)=0.1m/s，求（qiú）輸出量E_k的標（biāo）準不確定度u(E_k)。這時，不（bú）必去求偏導數得出靈敏係數，而是求輸入量的相對標（biāo）準不確定度u_rel(m)=u(m)/m=lg/1kg=1×10^-3，u_rel(v)=u(v)/v=(0.1m/s)/(100m/s)=1×10^-3，m的指數為（wéi）1，v的指數為2，則（zé）=(1×10^-3)²+(2×1×10^-3)²=5×10^-6，故u_rel(E_k)≈2.2×10^-3
    而u(E_k)=2.2×10^-3×(1/2)×1kg×(100m/s)²
    =2.2×10^-3×0.5×10⁴kg·m²/s²
    =11kg·m²/s²=11J
    如果p_i，隻是正1或負1，則在這一情況下:
    

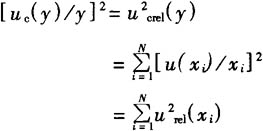
    這就是說:在這種情況下估計值y的相對合成標（biāo）準不確（què）定度，等於輸入估計（jì）值x_i的相對標準不（bú）確定度（dù）的方和根。舉例如下:
    設以鹽酸作為標準滴定溶液，用以測量某樣品中所含氫氧化鉀的質量分數W(KOH)，標準溶液的濃度c(HCl)=0.2(1±10^-3)mol/L(k=2)，則其標準不確定度u_rel[c(HCl)]=(1/2)×1×10^-3=0.5×10^-3。滴定終點消耗50mL，按（àn）所用的B級滴定管（guǎn）△=±0.6%(△為最大允（yǔn）許誤差)，由於通過兩次讀數之差（chà）得出，按正（zhèng）態分布考慮（lǜ），取包含因子k=3，得消耗體積V的相對標準不（bú）確定度u_rel(V)=(1/3)×0.6%×=0.28×10^-2。氫氧化鉀的相（xiàng）對摩爾質量來自國際1995年公布的相對原子質量表，其不（bú）確定度大大小於10^-5，可忽略不計，其值M_r(KOH)=56.10024，在本例計算中可（kě）取近（jìn）似為56.10，其修約導致的不確定度即可忽略。樣品質量m=10g，按所用天平和砝碼的相對擴（kuò）展不（bú）確定度U_rel(m)=3×10^-4，包含（hán）因子k=3，得其相對標準不確定度為u_rel(m)=1×10^-4。計算方程(測（cè）量模型)為:
    W(KOH)=f(V(HCl)，c(HCl)，M(KOH)，m)
        =(V(HCl)×c(HCl)×M(KOH))/m
代入輸（shū）出量的估計值（zhí）得:
    W(KOH)=56.1×10^-3
其相（xiàng）對標準不確（què）定度u_rel[W(KOH)]，可按u_rel(V)，u_rel(c)，u_rel(m)按方和根得出為:
    u_rel[W(KOH)]=
    
    =0.29×10^-2
如（rú）要求給出u[W(KOH)]，則再乘以W(KOH)的估計（jì）值:
    56.1×10^-3×0.29×10^-2=17×10_-5
    本例所討論的計算方（fāng）法，提供了不需求靈敏係數對合成標準不確定度的計算。
    7.7  當輸入量X_i之間出（chū）現了兩個或兩個以上的量x_i明顯相關時，是（shì）否可以不去（qù）計算協方差或是相關係數進（jìn）行合成標準不確定度的計算（suàn）？
    在《JJF1059》中隻提到協方差與相關（guān）係數的A類評定方法，將它與其他分量的方差相加進行合（hé）成。實際工作中，特別是在（zài）計量（liàng）學領域，采用A類評定是十分複雜的。我們可以按經驗，把輸入量x_i中強（qiáng）相關的那些分量(u(x_i)等也是由（yóu）若幹分量合成的，其中既有與其他（tā）輸入量強（qiáng）相關（guān）的分量，也有相互獨立的分量)，按強相關(r=+1)先行單獨合成作為輸出量不確定度u(y)的一個分量，然後把不（bú）相關的那些分（fèn）量（liàng）按彼此獨立合成為u(y)的第二個分量，最後將此兩分（fèn）量按彼此獨立來進行合（hé）成(參（cān）閱本講座6.18)。
    例如:在《JJF1059》合成標準不確定度u_c(y)的（de）評定中（zhōng），給過一個例子（zǐ），當標稱值為1kΩ的10個電阻器，用1個值為R_s的標準電阻器校準，設（shè）校準過程中的不確（què）定度（dù）遠小於R_s的標準不（bú）確定度u(R_s)而忽略（luè）不計（jì），校準證書給出u(R_s)=0.10Ω。現將此10個電阻器用電（diàn）阻可（kě）忽略的導線串聯構成一個10kΩ的參考電阻，其R_ref= f(R_i)=R_i(線性相加)。《JJF1059》中（zhōng）給出（chū）的電阻器的相關係數為r(R_i，R_j)=1，並（bìng）不可能是（shì）按A類評定的（de），因為（wéi）不存在多個標準器（qì）分別對這10個電阻器進行（háng）校準。這裏的（de）r(R_i，R_j)是按經（jīng）驗（yàn）得出的。通過經驗，當兩個(或多個)輸（shū）入量使用了同一個標準器或同一台測量儀器時，或使用了相同的參考數據，則它們之間存在極大的正相關。10個電阻器（qì）的校準正是這種情（qíng）況。在r=+1的情（qíng）況下，
    即線性相加，因而，所（suǒ）構成的10kΩ的R_ref的合成標準不確（què）定度
    u_c(R_ref)=u(R_i)
    =10×0.10Ω=1.0Ω
    但是，如果校準過（guò）程中帶來的不確定（dìng）度並非可（kě）忽略不計，例如在對這10個中每個電阻器校準過程中的標準不確定度為0.5Ω，10個這樣的分（fèn）量彼此獨立，大小也一樣，合成起來就是0.5Ω×=1.6Ω。它（tā）應按方和根與前（qián）麵（miàn）相關部分合成的1.0Ω合（hé）成的u(R_ref)==1.9Ω。
    7.8  合成標準不確定度u_c(y)的自由度計算中應注意什麽問題？
    合成標準（zhǔn）不確定度的自由度稱為有效自（zì）由度，符號為（wéi）v_eff輸出量估計值（zhí）y不確定度的各個分量u_i(y)的自由度不論是采用A、B兩類中的何種方法評定出的，u_i(y)的自由度與u(x_i)的自由度相同。不（bú）因為u(x_i)乘靈敏（mǐn）係數（shù）c_i之後而改變。計算式
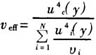    用於按u_i(y)計算的情（qíng）況。如有相關項，協方差（chà）隻出現在合成前u_c(y)的計算之中，在分母中不再出現。
    當（dāng）用相對標準不確定度分量u_rel(x_i)合成時，u_crel(y)的有效自由度隻（zhī）按下式計算:
    

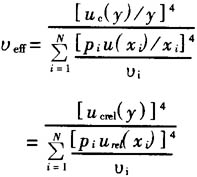
式中，p_i為x_i的指數，參閱7.6。