計（jì）量培訓：測（cè）量不確定度表述講座
國（guó）家質量技術監督局　李慎安

　　6.1  什麽叫不確定度的B類評定？
　　測量不確定度的評定方法主要分成兩大（dà）類。一類是（shì）用統計方法進（jìn）行評定，稱之為A類評定(參閱1.2)，而其（qí）他（tā）的非統計方法，統稱之為B類（lèi）評定，又稱之為非統計方法的評（píng）定（dìng），由此評定出來的（de）不（bú）確定度一般稱為B類不確定度或稱為B類標準不確定度。要（yào）注意的（de）是（shì）INC—1(1980)(參閱1.2)中以及《JJF1027》中都曾規定A類（lèi）不確（què）定度分量用（yòng）符號s_i，而B類不確定度分量用符號u_j表示，這一方式在《導則》以及《JJF1059》中已作了更（gèng）改，s隻是實驗（yàn）標準（zhǔn）偏差的符號（hào），當它作為（wéi）不確定度時，則（zé）不（bú）論是A類還是B類方法所得到，一律用u作為符號而隻以數字序號作為（wéi）下（xià）標相區別，一般則寫作u_i。從量值上說s=u，但含義不同（tóng）。
　　B類不確定度隻是其評定方法與A類不同（tóng），如此而已（yǐ）。在合成過程以及對測量不（bú）確定度的貢獻中完全（quán）一樣，它（tā）們都以標準偏（piān）差給出，也都可以評定其自由度（dù）。

　　6.2  用於評定B類不確定（dìng）度的信息一般有哪一些？
　　由（yóu）於B類（lèi）評定方法不是按統計方法進行（háng）的，一（yī）般不（bú）需要對被測量在統計控製狀態下(或是重複性條件下或複現性條件下)進行重複觀測，而是按現有（yǒu）信息加以評定。所用信息一般有:

　　(1)以前的觀測數據。
　　例如，對某一型號的測量儀器的重複性(參閱《JJF1001—1998》第7.27條)按A類評定方法，重複了20次觀測（cè），得出了其單次示值的分（fèn）散性，即重複性標準偏差s_r。由於這個s_r的自由度υ=20-1=19，一般（bān）來（lái）說，也是充分可靠的了（le）。所以，這個數（shù）據（jù）可以用作該測（cè）量儀器進行一次、或重複幾次測量結果的不確定（dìng）度評定信息。
　　但是，同一型號（hào）的某測量儀器的（de）重複性如果彼此並不一定接近，例如，有1/3或（huò）1/4左右（yòu）的差，那麽，如果我們對例如隻有三台這樣的測量儀器，分別各進行了20次觀測試驗，並分別得出它們（men）的重複性分別為s_r1=3.4，s_r2=2.4，s_r3=2.9。這（zhè）三（sān）個標準偏（piān）差可認為充分可靠，而（ér）這樣（yàng）的差別則是反映了儀器（qì）本身重複性的（de）不同。這（zhè）一現象，說（shuō）明不能（néng）用一台（tái）儀器的s_r代替同類型的其他（tā）儀器的s_r使用。如果，如上（shàng）例，把這（zhè）三個s_r取平均值=2.9，那麽其標準偏差按貝塞爾公式
    自由度為2，因此，拿2.9作為其他同類型（xíng）測量儀（yí）器的單次測（cè）量的分散（sàn）性標準差也是不行的。這個例子說明:對以前的觀測數據應加以分析，看其是否可用於當前的測量結果。

　　(2)對（duì）有關（guān）技（jì）術資料和測量儀器特性的（de）了解和經驗。
　　例如50 mm的量塊，其中心長度最大允許示值誤差，對於零級來說是±0.25μm，一級（jí）是（shì）±0.50μm、二級是±1.00μm。僅是這樣的（de）信息是不（bú）夠（gòu）的，還應了解在二級量塊中是（shì）不會出現（xiàn）示值誤差在±0.50μm內的（de）量塊；同（tóng）樣（yàng），在一級量塊中，也決（jué）不會（huì）出現示（shì）值誤差（chà）在±0.25μm內的量塊。原因是在成批生產出同一（yī）標稱尺寸的量塊後，按最大允許示值誤差把（bǎ）±0.25μm者作為零級挑出，把從±0.26μm至±0.50μm者（zhě）挑出作為一級，如（rú）此（cǐ）類推。因（yīn）而雖然有最大允許（xǔ）示值誤（wù）差的信息，按上述特性，隻是接（jiē）近兩點分布，有了這一信息（xī），就可以評（píng）定其標準不確定度了。

　　(3)生產部門提（tí）供的（de）技術說明文件
　　例如對某些裝備了玻（bō）璃短標尺的測長光學儀器，一般，生產廠是給出了該尺（chǐ）的線膨（péng）脹係數的，我們就（jiù）可以依據它對由於溫度測量（liàng）導致的不確（què）定度進行評（píng）定。

　　(4)校準證書、檢（jiǎn）定證書或其他文件提（tí）供的數據、準確度的等別或級別，包括目前還（hái）暫在使用（yòng）的極限誤差等。
　　校準是指在規定條件下，為確定測量儀器或（huò）測（cè）量係統所（suǒ）指示的量值，或實物量具或參考物質所代表（biǎo）的量值，與（yǔ）對應的由標準所複現的量值之間關係的一組操作。簡而言（yán）之，即為確定測量儀（yí）器示值誤差的（de）一組操作，或給出示值的一組操作。例如對標準硬度塊的定（dìng）度，對標準砝碼、量（liàng）塊、標準電池的（de）賦值（zhí）等。當然，在校準證（zhèng）書中必定要給出其校準結果的不確定（dìng）度（dù），甚至還要給出其自由度。給出該測量儀（yí）器所屬的等別(order)或(和)級別(class)，這些都是據以評定標準不（bú）確定度的極為常見的信息（xī）。
　　至於極限（xiàn）誤差，目前還（hái）在JJG2009《射頻與微波功率計量器具檢定係統》、JJG2010《射（shè）頻與微波衰減（jiǎn）計量器具檢定係統》、JJG2016《粘度計（jì）量器具（jù）檢（jiǎn）定係統》、JJG2027《磁感應強度計量器具檢定係統》等為數尚（shàng）不少的技術規範中使（shǐ）用，這是（shì）我（wǒ）國50年代以來的作法（fǎ），由於對極限誤差的評定缺乏統（tǒng）一的規範，導致其含義不（bú）確切。當前不應再使用這一概念來表述測量結（jié）果，但（dàn）對早已存在的規範，未修訂以（yǐ）前，還應可以作為評定標（biāo）準不確定度的依據。

　　(5)手冊（cè）或（huò）某些資料給出（chū）的參考數據及其不確定度。
　　例如手冊上給出的基本（běn）物理常量、阿伏加德（dé）羅常數L=(6.022 136 7±0.000 003 6)×10²³ mol^-1，並聲明±號後之值為標準偏差，其自由度為17。
    又如國際上1992年公布的相（xiàng）對原（yuán）子（zǐ）質量。例如對於碳原子A_r(C)=12.011(1)，括弧中的1表示相對原子質量值的標（biāo）準偏差為0.001。可惜的是沒有指明（míng）不確定度的（de）自（zì）由度。但這可（kě）用於對不確度分量的（de）評定。

　　(6)技術規範中對某些測量方法所規（guī）定的（de）重複性限r或複現性限R。
　　在一些檢測方法的國家標準或其他技術（shù）規範中給出的r或R一方麵用於查明實驗過程是（shì）否處於所規定（dìng）的狀態，是否出現過大的誤差，另一方麵，說明了這一方法的不確定度（dù）。
　　B類標準不確定度u(q_i)的二（èr）次方，可簡稱為B類方差。

　　6.3  當已知擴（kuò）展不確定度U及包含因子k時，如何（hé）評定其標準不確定度？
　　例如（rú）當前（qián）對圓錐量規、錐度（dù）儀器、熱（rè）電偶、維氏硬度計、色溫度儀器、發光強度計（jì）、核素（sù）活度計等類，在其檢定係（xì）統中均明確規定校準（zhǔn）結果要按k=3給出擴（kuò）展不確定度U。而例如超聲（shēng）功率計（jì）、橡膠硬度計、黑白密度計等，采用k=2給出擴展不確定度U。在這些情況下，隻要用U除以k即可（kě）得出標準不確定度。例如:某交流數字電流表，流（liú）量上限為10A，相對擴（kuò）展不確（què）定度為5×10^-4，k=3，則其相對標準（zhǔn）不確定度（dù）u_rel=5×10^-4/3=1.7×10^-4。

　　6.4  如果檢定、校準證書上給出總體標準偏差σ的倍數時，如何（hé）評定標準偏差？
　　當前還（hái）有不少測量儀器仍沿用50年代以來的習慣，用總體標準（zhǔn）偏差σ及其倍數表示校準結果的可靠程度。例如:真空測（cè）量儀器、燃燒熱測量儀器、電導流量儀器、水流（liú）量測量儀器、某（mǒu）些壓力測（cè）量儀器等。本來σ隻是一種（zhǒng）理想概念（niàn），在計量學中的總（zǒng）體（tǐ）指重複性條件下，對同一被測量進行了無限多次的重複觀測，通過這無限多個觀測結果按（àn）下式:
　　計算出來的，式中μ為對（duì）被（bèi）測（cè）量Q進行無限多（duō）次的算術平均值，稱（chēng）為總體均值，N是重複（fù）觀測次數，為無限大。由於實際測量中的重複次數n是極為有限的，按貝塞爾公式算出的實驗標準偏差s隻（zhī）是σ的一個估計，應（yīng）該說，把s等同於σ是不合理的，s本身還有不確定度，而σ的不確定度為零。但是（shì），現在在一些測量儀器既已用了（le）σ的情況下，我（wǒ）們在（zài）評定標準不確定度（dù）時，可以把σ直接作為標準不確（què）定度（dù）u處理，即從量值上說σ=u。又如，射頻與（yǔ）微波功率計、脈衝參數計量儀器、真空（kōng）測量儀（yí）器等，它們用3σ給出時，采用其三分之一即獲得標準不確定度（dù）。對於（yú）那些燃燒熱、氣體流量、石油螺（luó）紋測量儀器等，它們（men）用2σ給出時，采用其一半即獲得相應標準不確定度。
　　對於例（lì）如液體閃爍放射性活度測量（liàng）儀器、質（zhì）量測量儀器等，給出置信概率為99.73%的情況下，由於原假設為理想的正態分布，而且所得到的合（hé）成標準不確定度又十分可靠，在這一情況下給出了上述置（zhì）信概率，盡管（guǎn）從實際上說不十分合理，雖原為（wéi）3σ的含義在進行不確定度評（píng）定（dìng）時，可按U₉₉處理，即除以2.6，但也（yě）未必不可以除3，前者偏保守即稍可靠一些。作這（zhè）種評定時，自由度可估計大一些（xiē），而（ér）用除以3來評（píng）定u時，自由度就不能估計得太大。

[page_break]

　　6.5  已知（zhī）U_p的（de）情（qíng）況（kuàng）下，對標準不確定度的評定如何？
　　從現在起，將會（huì）越來越多地在（zài）校準證書上給出校準結果的（de）擴展不確定（dìng）度U₉₅，或U₉₉，這樣就十分明確地交代了置信概率p的大小（xiǎo）。如果沒有特（tè）殊說明，一般總按正（zhèng）態分布考慮（lǜ），並據以評定其標準（zhǔn）不確定度。在正態分布情況下，置信概率p與（yǔ）包含因子k_p之間（jiān）的對應關係為:
　　p=0.90    k_p=1.64；
　　p=0.95    k_p=1.96；
　　p=0.99    k_p=2.58。
　　例如肖氏（shì）硬度計用U₉₅，而(273.15～903.15)K溫度計用U₉₉。顯然，如給出的是（shì）U₉₅，則u=U₉₅/1.96，如（rú）給出的是U₉₉，則u=U₉₉/2.58。

　　6.6  如果校（xiào）準證書上既給出了U_p，又給出了（le）其自由度（dù）υ，應如何評定其標準不（bú）確定度u？
　　在《JJF1059》中，推薦在給出擴展不確定度U₉₉或U₉₅時（shí），同時給出其自由度。當這些信息已在校準證書中（zhōng）給出後，使用者不僅可以更有把握地給出標準不確定（dìng）度u，而且這個u之值會比（bǐ）6.5所評定出的要小一些，對不確定度評定是有利的。
　　當有了自由度υ以後，可以按以下t值在表格中查出k_p=t_p(υ)這個值。例如:已知的自（zì）由度υ=10，采用的置（zhì）信概率p=0.99，表中給出k_p=3.17，這個（gè）值比上述6.5中的2.58大了不少，約五分之（zhī）一。這樣，通（tōng）過U_p/k_p所得的標準不確定度就會比用k=2.58除得出（chū）的值要小約（yuē）五分之一。油（yóu）水不少!

　　6.7  當已知量X之值x分散區間的半寬為（wéi）a，且x落在（zài）x-a至x+a區間的概率p為100%，即全部落在此範圍內，如何評定（dìng）標準不確定度（dù）u(x)？
　　在x±a內包含了X的全部可能值。a處於x的兩側，而（ér）且，x處於已知區間x-a至x+a的中央。拿a作為（wéi）擴展不確定度U(k=3)或是U₉₉未必不（bú）可以（yǐ），隻（zhī）是不太確切，也不很可靠（kào）。p=100%可認為接近99%，而k=3則不一定確切。在（zài）這一情況下（xià）要評定其標準不確定度u(x)時，與X可能值的分布類型關（guān）係（xì）很大，因（yīn）而必須對其分布作出一（yī）個近似的估計，需要有一（yī）定的經驗（yàn）。分布的情況與包含因子k的關係是:越接近(向正態分布趨近)正態分布，k值（zhí）越大。從兩點（diǎn）分布到正態分布，k值由1增加到3。
　　接近正態分布:  k=3    

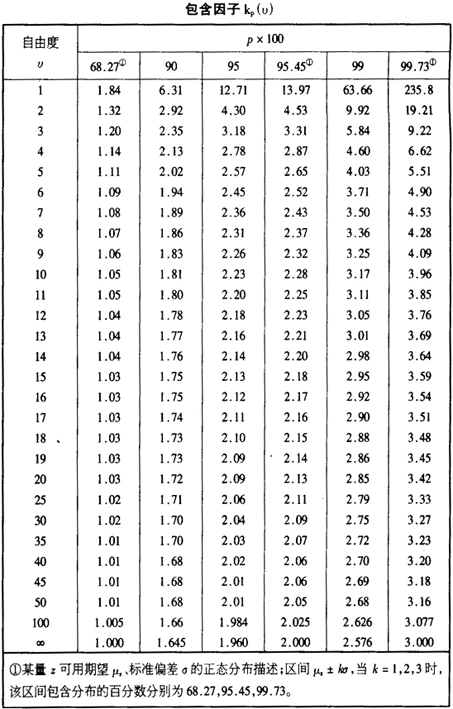
　　三角分（fèn）布:  k=≈2.45
　　梯形分布:  k=2
　　矩形分布:  k=≈1.73
　　反正弦分（fèn）布:k=≈1.41
　　兩點分布:  k=1
　　以上梯形分布指其上底與下底之比β=0.71的較為多見的標準狀態（tài）。當包含因子k增大，評定出的標準不確定度u(x)=a/k就減小。
　　分散區間的半寬a可以理（lǐ）解（jiě）為可能出現的誤差極限值之模。即絕對值最大的誤差，一般用誤差（chà）限這（zhè）個概念。但表述為（wéi）誤差限時，帶（dài）有正負（fù）號(±)，例如測（cè）量儀器的最大（dà）允許誤差。
　　一般用a_-，表示（shì）小於x的那（nà）個下界，而用a₊表示（shì）大於x的那個上界，或（huò）稱為x的下限（xiàn）、上限值。

　　6.8  如何對分（fèn）散區間x-a至x+a範圍內，x可能值的分布類別進行估計？
　　如果測量（liàng）結果x是幾個觀測值的平均值（zhí）(例如三個以上)(經常用（yòng）算術平均值作為測量結果)，則其分布必定是正態的（de）。如果被測量Y是由兩三個以上的分量按線性合成時(例如相加)，而這些分量彼此的（de）大小又比較接近，則y的分布是接近正態的，如果Y是由兩個分（fèn）量線性合成，而這兩個分量接近，且是三（sān）角分布，則y的（de）分布也會是正態的。自由度的大小與分布無關，不能（néng）作為考慮分布的依據。
　　在（zài）缺乏任何其他（tā）信息的情況下，一般估計為矩形（xíng）分布(均勻分布)。但如果已知Y的可能（néng）值出現在a_-至a₊中心附近的可能性大於接近區間邊界時，則可按三角分布評定（dìng）u(y)。
　　以下給出幾種分布類別（bié）的情況:

　　(1)正態分布
　　a)重複性條件或複現（xiàn）性條件下多次測量的算術平均值或加（jiā）權平（píng）均值的分布；
　　b)被測量Y在校準證書中用擴展不確定度U_p給出，而（ér）對其分布又沒有特殊說明時，估計值y的分布；
　　c)在被測量Y的合成標準不確定度u_c(y)中，相互獨立的分（fèn）量u_i(y)較多（duō），它們之間的大小也比較接近時，y的分布；
　　d)在（zài）被測（cè）量Y的合成標準不確定度u_c(y)中，相互獨立（lì）的分量u_i(y)中，存在兩個（gè）界限值（zhí）接近的三角分布，或4個界限值接近的（de）均勻分布時；
　　e)被測量Y的合成標準不確定（dìng）度u_c(y)的相（xiàng）互獨（dú）立的分量中，量值最大的分量(起決定（dìng）作用的分量)接近正態分布時。

　　(2)矩形(均勻)分布
　　a)數據修約導致（zhì）的不確定度；
　　b)數字式測量儀器（qì）分（fèn）辨力導致的不確定度；
　　c)測量儀器由於滯後、磨（mó）擦效應導致的不確定度（dù）；
　　d)按級使用的數字式儀表、測量儀器（qì）最大允許誤差導致的（de）不確定度；
　　e)用上、下界（jiè）給出的線膨脹係數；
　　f)測（cè）量（liàng）儀器度盤或齒輪回差引起的不確定度；
　　g)平衡指示器調零（líng）不（bú）準導致的不確定度。

　　(3)三角分布
　　a)相同修約間隔（gé）給出的兩獨（dú）立量之和或差，由修（xiū）約導致的不確定度；
　　b)因分辨力引起的兩次測量結（jié）果之和或差的不確定（dìng）度；
　　c)用替代法檢定標準電子元件或測量衰減（jiǎn）時，調（diào）零不（bú）準導致的不確定度；
　　d)兩相（xiàng）同均勻分布（bù）的合成。

　　(4)反正弦分布(U形分（fèn）布)
　　a)度盤（pán）偏心引起的（de）測角不確定度；
　　b)正弦振動引起的位移不確（què）定（dìng）度；
　　c)無（wú）線電中失配引起的不確定度；
　　d)隨時間正餘弦變（biàn）化的溫度不確定度。

　　(5)兩點分布
　　例如，按級使用量塊時，中（zhōng）心長（zhǎng）度偏差導致的概率分布（bù）。

　　(6)投影分布
　　a)當Y_i受到（dào）1—cosα(角（jiǎo）α服從均勻分布)影響時，y_i的概（gài）率分布；
　　b)安裝或調整測量儀器的水平或垂直狀態導致的（de）不確定度。

　　(7)無法估計的分布（bù）
　　大多數測量儀器，對同（tóng）一被測量多次重複測量，單次測量示值的分布一（yī）般不是正（zhèng）態分布，往（wǎng）往偏離甚遠（yuǎn）。如軸尖支承式儀表示值分布，介（jiè）於正態分布與均勻分布之間，數字電壓表示值分布呈雙峰狀態，磁電係儀表的示（shì）值分布與正（zhèng）態分（fèn）布相差甚遠（yuǎn）。

[page_break]

　　6.9  當被測量X的最佳估（gū）計值x並不（bú）處於其可能值（zhí）分散區間2a，即(a₊-a_-)的中點時，如何評定（dìng）標準不確（què）定度u(x)？
　　這（zhè）時，由於x不處於a_-至a₊的中心，X可能值分布在此（cǐ）兩區間內（nèi）的概率是（shì）不一定相等的，也（yě）一（yī）般不會是對稱的，在缺乏用於可靠（kào）判斷其分布（bù）狀態（tài）的信息時，按矩形分布處理，可近似地采用:
　　上式中的b₊，b_-為:
　　b_-=x-a_-
　　b₊=a₊-x
　　且b_-≠b₊
　　計算式中的分母為(2)²，2是取分散區間的一半，是按矩（jǔ）形分布給出的（de）包含因子k。
    有時也可以對這類不對稱（chēng）的界限采用修正的方法，即對最佳估計x加以修正，修正值的大小為（wéi）(b₊-b_-)/2，在修正後，x就處於分散區間的中心（xīn）x=(a_-+a₊)/2，而其半寬a=(a₊-a_-)/2。即可按6.7所述方式評定u(x)。

　　6.10  測量儀器分辨力導致的標（biāo）準不確定度如何評（píng）定？
　　分辨力是顯（xiǎn）示裝置分辨（biàn）力（lì）的簡稱。按《JJF1001》定義（yì）為:顯示裝置能有效辨別的最（zuì）小示值差。對於數字式顯示裝置，即變化末位一個有效數字時（shí），其示值的變化，所謂步進量。
　　分辨力導致的示值誤（wù）差限為±0.5個步進量。即其分散（sàn）區間的半寬a為0.5×步（bù）進量。由於（yú）被測量可能值（zhí）出（chū）現在這一分（fèn）散區間之內的任一點的概率相等，應估計其分布類型為矩形。設分辨（biàn）力為δx(按《JJF1059》給出（chū）的符號)，則由此而帶來的標準不確定度為0.5×δx/≈0.29δx。

　　6.11  對量值修約所導致的標準不確定度如何評定？
　　對（duì）一個量（liàng）值修約以後，必定帶來修約誤差，修約誤差等（děng）於修（xiū）約後的值減修約前的值。例如:100.046 50 g修約成為100.046 g，即保留到1mg的水平，其修約誤（wù）差為100.046 50 g-100.046 g=0.0005g=+0.5mg。修（xiū）約誤差既可為正（zhèng）也可為負值。如把100.045 50 g修約到小數點後（hòu）第3位，按（àn）一段修約規則，也得到（dào）修約後之值為100.046g，這時的（de）修（xiū）約誤差為-0.5mg。我們從一個（gè）已修約後的值無（wú）法（fǎ）看出它在修約（yuē）前（qián）是（shì）多大。但是，可（kě）以（yǐ）判斷其修約誤差限（xiàn）。從而修約所帶來的誤差（chà）限等（děng）於半個修約間（jiān）隔。所謂修（xiū）約間隔，在國（guó）家標準GB8170—1987《數值修約規則》中，定義為修約值的最小單（dān）位。也就是說，修約後之值隻（zhī）能是其整數倍。因此，上例中給出的100.046g，其修約間（jiān）隔為0.001g即1mg。對於一個已修約的（de）值，如果不是0.5和0.2修約間隔(這（zhè）種情況極少使用)，其修約間隔必定是這（zhè）個數值的末位為1的值。例如:73.684mm，其修約間隔為0.001mm；73.6845mm的修約間隔為0.0001mm。
　　修約導致修約誤差。對於一個已修約之值，我們雖不知道修約（yuē）前之值，根據其最大不超過半個修約間隔及均勻分布的估計（jì），修（xiū）約導致的標準偏差不超過:0.5×半個修約間隔/≈0.29修（xiū）約（yuē）間隔。當從某種資料查到的近似值沒有任何其他信息用以評定（dìng）其標準不確定（dìng）度時，按該（gāi）數據給出的值到了哪一位，進行修約不確定度的評定往往是唯一的辦法。

　　6.12  按重複性限r與複限性限R如何評定該條件下的重複性標準（zhǔn）偏差s_r和複現性標準偏（piān）差r_R？
　　按現行國際標準ISO5725—1994《測量方法與測量結果（guǒ）的準確度》給出的重複性限r和複（fù）限（xiàn）性限R的定義是，在重複性條件下或複現性條件下（xià），兩次測（cè）量結果（guǒ）之間的差，以95%的置信概率，不致超過的值（zhí）。當製定（dìng）了某種測量程序和條件之後，在這一條件下的測（cè）量（liàng）結果間的分（fèn）散（sàn）性、重複性標準偏差或複現性標準偏差，是（shì）可以通過實驗按統計方（fāng）法評定的，得到的結果就是s_r或s_R。如果自由度充分大(例如超過20)，而且在（zài）重複測量結果的分布又接近（jìn）正態的前提下，s_r與（yǔ）r之間以及s_R與R之間有:
　　r=2.8s_r
　　R=2.8s_R
　　當在（zài）有關技（jì）術規範（fàn）中給出了r或R時，按上述關係可以計算出（chū）s_r或（huò）s_R作為標準不確定度。

　　6.13  按校準證書已知（zhī）某測量儀器的等別時，如何評定其標準不確定度？
　　對於那些分等的測（cè）量儀器，在其校準證書中，一般（bān）均給出了被校準測量儀（yí）器屬於哪個等（děng），而往往不再給（gěi）出校準結果的不（bú）確定（dìng）度。等是按校準結果不（bú）確定度大小劃分的一種檔次，例如（rú）量塊、活塞壓力計、標準電池等。給出了等（děng）別，實質上就相當於說（shuō）明了其不確定度不超過某個限值。例如（rú）對於50mm的量塊，二（èr）等（děng）的（de）不確定度不大於0.09μm(p=0.99)，有了這一信息後就可以按6.5進行評定，隻不過（guò）往往在校準證書上隻給等別而（ér）不給（gěi）出相應的（de）U和U_p。這時，就得查有關的檢定係統或檢定規程了。

　　6.14  按校準證書已知被檢測儀器的級別時，如（rú）何（hé）評定其標準偏（piān）差？
　　級的概（gài）念是按測（cè）量儀器(包括實（shí）物量具)示值誤差（chà）劃分的檔次（cì）(包（bāo）括相對誤差)。因此，明確了級別，實（shí）質上也就是說明了其示值誤差不（bú）致超出的界限(上下界)。例如:50mm的二級量塊，其中的長度（dù）偏差(最大允許誤差)限為±1μm。如果我們（men）是按其中心長度的標稱值來使用這個量塊（kuài），所導致的標準不確定度就隻能按±1μm這一信息，再加上它（tā）是（shì）兩點分布(參閱6.8)，其標（biāo）準不確定度為1μm(注意這時不再用（yòng）正負號)。級別（bié）所對應的誤差限往往也需另查資料。
　　有時，級（jí）別是按引用誤差(相對示值誤差的一種)之數（shù）值（zhí）給出的（de）。例如證書上給出符合1.5級壓力表，這個級別的引用誤差是1.5%，並（bìng）非測量不確定度（dù）。引用誤差的方便之（zhī）處在於，對於不少指（zhǐ）針式測量（liàng）儀器來說，特別是多量限的測量儀器，不論是在（zài）量限內的哪一點上，其引用誤差都是同一（yī）個值。在不確定度評定中，可據以將它作為示值誤差分散區間（jiān）的半寬(相對值)，再按6.7所述評定。

　　6.15  什麽情況下，B類（lèi）評定方法所（suǒ）得出的標準不確定度的自由（yóu）度可估計為無限大？
　　自由度是用於說明（míng）標準不（bú）確定度的可靠性的，越可靠，自由度越大。因（yīn）此，當我們用非統計方法（fǎ）評定出（chū）的結果十分可靠（kào）時，就可估計其（qí）自（zì）由度為無限大，例如:
　　(a)校準（zhǔn）證書上給出了校準結果的擴展不確定度U或U_p，該標準測量儀器穩定性極好或校（xiào）準時間並不太長，保存（cún）條件也較理想，其（qí）值不致（zhì）有明顯變化。
　　(b)按測量儀（yí）器的最大允許誤（wù）差或級別所評定出的標準不確定度。
　　(c)按測量儀器的等別的不確定度檔次界限所作出的評定。
　　(d)按（àn）測量儀器引用誤差或其相應級別作出的（de）評（píng）定。

　　6.16  符（fú）號Δu(x_i)指什麽？
　　在《GUM》以及《JJF1059》中均（jun1）用了這（zhè）一（yī）符號，但未（wèi）明確其含義，u(x_i)是被測量Xi的標準不確定度，這是上述文件均已明（míng）確（què）的。加（jiā）了一個Δ，則表示u(x_i)的誤差限，但是用標準偏差給出的值。這裏，Δ這個符號用得不太標準。Δu(x_i)可以認為（wéi）是（shì）指u(x_i)的（de）不確（què）定度，即不確定度的不確定度，或標準（zhǔn）偏差的標準偏差。

　　6.17  符號Δu(x_i)/u(x_i)或σ[u(x_i)]/u(x_i)的含義如何？為什麽（me）用它來評定B類標（biāo）準不確定度的自（zì）由度？
　　Δu(x_i)的含義已如6.16所述，σ[u(x_i)]的含義是用（yòng）了總體標準偏差σ來代（dài）替Δ，指可靠的標準偏差（chà）之（zhī）值。
　　不管對標準偏差的評定方法如（rú）何，A類還是B類，所得出（chū）的（de）標準偏差均存在一個可靠性（xìng）如何的問題。
　　基於通過重（chóng）複測量的統計方法不一定就比非統計（jì）方法好，就平均值的標準偏差s()而言，它是正態分布隨機變量q的n次獨立觀測值平均值的實驗（yàn）標準偏差（chà）。量s()是個統（tǒng）計量，它是總體標準偏差σ()的估計，σ()是的概率分布的標（biāo）準偏差，即是無限多次重複觀測得到的值分布的標準偏差。s()的方差σ²[s()]近似地為:
　　σ²[s()]≈σ²()/2υ
　　其中，υ=n-1是s()的自由度。因此，可以取s()的相對標準偏差σ[s()]/σ()作為s()的（de）相對（duì）不確定度的度量，它近似地等於[2(n-1)]^-2。這（zhè）是的不確定（dìng）度的不（bú）確定度，完全由於有限次數n不夠大（dà）而引（yǐn）起。例如在n=10時，它等（děng）於約24%。而在非統計方法評定（dìng）的標準偏差中（zhōng），根據自由度的定義，當自由（yóu）度υ在t分布出現（xiàn）時，它是方差s²()的（de）不確定度的度量，有
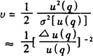　　方括號中給出的（de）是u(q)的相對不（bú）確定度，對B類評定而（ér）言，它是個主觀量，其值是按可利用的信息判斷（duàn）的。
　　例如:考慮到輸入估計值x_i及其標準不確定度u(x_i)的信息，判斷u(x_i)的值大約不可靠到25%，就意味其相對不（bú）確定度△u(x_i)/u(x_i)=25%，代入上式，得υ_i=(0.25)^-2/2=8。如（rú）果判（pàn）斷u(x_i)之值大約隻有（yǒu）50%可靠，也就是50%不可靠。代入上式，算出υ_i=2，實際工作中，一（yī）般隻估計出其不可靠的百（bǎi）分數，查（chá）下表即可（kě）:
    

　　當（dāng）前，有些文獻把（bǎ）“可（kě）靠”與“不可靠”的含義（yì）弄混淆（xiáo）了，例如:“自由度由於標準不確定（dìng）度有25%可靠（kào），υ=8”。顯然，這個25%應是“不可靠（kào）”而非“可靠（kào）”。此外，這裏所（suǒ）用“可靠”一詞，隻是一個通俗的概念。

　　6.18  相關係數r是否可以進行B類評定？
　　在計量學領域中（zhōng）的極大多數情況下，相關（guān）係數r的（de）評定並非（fēi）通過A類方法（fǎ）進行而是通過B類方法進行的。例（lì）如:用一個標準砝碼來校準若（ruò）幹個標稱值相同的工作用砝碼，然後用這（zhè）些工作砝碼去校準大秤量的衡器時，這些工作（zuò）砝碼的標準不（bú）確定（dìng）度雖（suī）然都相等，但存（cún）在很大的相關性。用同一標電阻器校準若幹（gàn）個標（biāo）稱值相同的電（diàn）阻（zǔ）器，將它們（men）串聯（lián）起來用於較大電阻的檢定時也同樣如此。
　　以上兩例情況基本相（xiàng）同。檢（jiǎn）出的電阻器校準值的不確定度基本由兩（liǎng）個分量構成，一是標準電阻器的不確（què）定度，二是校準過程中引入的不確定度。前（qián）者，按經（jīng）驗是正強相關，r₁=1，但後者（zhě）按（àn）經（jīng）驗，彼此獨立，不相關，r₂=0，這種評定屬於B類方（fāng）法。例（lì）如:10個被校電阻器串聯，則可將它們串（chuàn）聯後電阻值的不確定度也分（fèn）成兩（liǎng）部分，把強相關的r₁=1的哪一部分先合（hé）成，即取10倍的標準電阻不確（què）定度，相（xiàng）互獨（dú）立的第二部分另行合成(方和根)，實際為倍的一次校準不確定度。有關合成問題（tí）將在本講（jiǎng）座後（hòu）麵有關部（bù）分詳述。