圖1  新（xīn）莽銅嘉量

如果說栗氏（shì）量（liàng）隻有一段並不詳盡的文字記載，劉歆卻在它的基礎上經過再創造，實實在在地製造出一件曠世（shì）佳作。新莽銅嘉量有十分詳盡的刻銘:斛量正麵器壁上刻81字詔文(見圖2)，大意是:唐堯、虞舜的美（měi）德傳到莽（mǎng），建立了新朝。統一了律度量衡，故昭告天下，萬世永遵，享傳億年。背麵又（yòu）在五個單獨量的外壁上加刻（kè）每一（yī）量器的直徑、深度（dù）及計算容積，總共二百四十多（duō）字。在文（wén）博學（xué）家們眼裏，古代器物上的刻銘，字字千金。而新莽銅嘉量上，不但刻銘詳盡，而且包含著深邃的科技含量，其（qí）價（jià）值（zhí）該有多大啊!那麽我們就（jiù）來看看新（xīn）莽銅嘉量是如何既繼承（chéng）古製，又（yòu）有創新（xīn）的。

①關於其形（xíng）

栗氏（shì）量集升、豆、鬴三量於一器，並簡（jiǎn）要說明了器（qì）的尺度、容積以及重一鈞。新莽銅嘉量則是集龠、合、升、鬥、斛五量，每一量都有詳盡的尺寸及計算容積（jī）。《漢書·律曆誌》另注明“重（chóng）二鈞”。②關於“內方尺而圜其外”與（yǔ）嘉量的“庣旁”栗氏量記:“內方尺而圜其外，其實一鬴，”嘉量刻銘（míng）:“方尺而圜其外，庣(tiao)旁九厘五毫。……容十鬥。”栗（lì）氏量與新莽銅嘉量皆采用先取一正方（fāng）形，每（měi）邊長一尺，在正（zhèng）方形外作圓。但栗氏量所用的尺是多長，一鬴的容積是多少，都（dōu）已無法知道了（le）。而嘉量度量衡三個量的量值必須（xū）體現漢代的實際情況:一尺是23.1厘米，一斛之積是1620立方寸。要滿足一斛之積是1620立方（fāng）寸，圓麵（miàn）積就必須是162平方寸，如果圓的大小是方一尺作外接圓，那麽實際計算所得的圓麵積就是157平方寸（cùn），比所要求（qiú）的少了5平方（fāng）寸。如何做到既（jì）要與栗氏量“方尺而圓（yuán）其外（wài）”的提法相同（tóng），又能保證圓麵積達到162平方（fāng）寸呢？這一點確實是一個很（hěn）大的難題（tí）。劉歆不但是一位古文經學大師，而且還精通律曆學，對數學也（yě）有很（hěn）深的造（zào）詣，他想，隻要把（bǎ）圓徑加大五平方寸，圓麵積不（bú）就加大了嗎。在他的（de）苦苦尋求下，又經過反複運算，終於提出了（le）一個最佳方案（àn），即在（zài）正方形的對角線兩（liǎng）端各加上9厘（lí）5毫，就能與162平方寸相符了。劉歆（xīn）還為這個“九厘五毫”專門取了一個（gè）特殊的名字“庣旁（páng）”。這個方法真是太巧妙了，這時劉歆才（cái）大大地鬆了一（yī）口（kǒu）氣，同（tóng）時也為（wéi）自己的創造感到非常滿意。③關於黃鍾（zhōng）律栗氏量又說:“聲中黃鍾之宮”，我（wǒ）們再來看（kàn）看嘉量的刻銘（míng）是如何與它相對應的吧？嘉量每一器分銘前都加有一個“律”字，如律嘉量斛（hú）、律嘉量鬥等。律嘉量（liàng）龠銘文說（shuō）得更具體:“積八百一（yī）十（shí）分，容如黃鍾（zhōng）”。二者（zhě）說法雖不完全相同，但其承傳關係卻十分清楚。關於“聲中黃鍾之宮”，當然不是說敲擊栗氏量發（fā）出的聲音，與黃鍾律之宮音相合。劉歆根據他的理解，認（rèn）為應該是“栗氏量尺（chǐ）”與黃鍾律管的長（zhǎng）度有某種內在的聯係。最後提出了以黃鍾律管、累黍（shǔ）定度量衡的理論。這一理論的（de）提出，在中（zhōng）國度量衡史上影（yǐng）響極（jí）大，以（yǐ）致其後為此研究、討論了1000多年。關於黃鍾、累黍定度量（liàng）衡，已有許（xǔ）多文章做過論述（shù），這裏不再（zài）展開。古代的量器，很難達到較高的精確度，故有“以度數審其容”之說。新莽嘉量就是一件以（yǐ）尺度來計算（suàn）容積的高科技產品。嘉（jiā）量銘文:“冥(冪)百六十二寸，深尺（chǐ），積千六百二十寸，容（róng）十鬥。”嘉量各器都是（shì）圓筒形，要計算它們的容（róng）積，就要牽涉圓周率的問題。劉歆用的是什麽圓周率呢（ne）？可惜銘文沒有提到，他使用的圓周率及求圓周率的方法，就成了千古之謎。在其後二百多年的三國魏時，數學家劉徽最早對新莽銅（tóng）嘉量（liàng）刻銘中的計算容積作了研究。他認為劉歆在設計嘉量時，對庣旁的設置已精確到了（le）厘毫，在計（jì）算容積時，是不會使用《周髀算經》裏說的“徑一周三”這樣粗略圓周率的。但是他究竟用的是什麽圓周率呢？劉徽為了對（duì）新莽銅嘉量作考校（xiào），經（jīng）過（guò）反複研究，終（zhōng）於發明了用割圓術來（lái）求圓（yuán）周率，再經過無數次運算，得到圓周率是3.14，為此（cǐ）他成為中（zhōng）國運用正確方法求圓周率的首創者。緊（jǐn）接著又以他（tā）求得的圓周率去核算嘉量的圓麵積，得到的數值為（wéi）“冪一百（bǎi）六十一寸（cùn）有奇”，即不到162寸。可惜（xī）他沒有再（zài）作更進一步的（de）探討。在劉徽之後的（de）200多年，即南北朝時期。有一天，數學家祖衝之在皇宮中見到這件新莽（mǎng）銅嘉（jiā）量，他十分興奮，大為驚歎道（dào），銘文刻得如此詳盡，真是了不起。祖衝之畢竟是一位數學家，立刻想到（dào）這件嘉量計算精確的程度如（rú）何?自（zì）己為何不按照器壁上刻的銘（míng）文親自驗算（suàn）一下呢。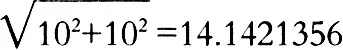要計算斛的容積，第一步（bù）先（xiān）算出它的直徑，即一尺正方形對（duì）角線長為寸，庣旁九厘五毫(0.095寸)，圓麵積的直徑為14.1421356+2×0.095=14.3321356寸（cùn），銅斛的半（bàn）徑是7.166寸，圓麵積即銘文中所說162平方寸，祖衝之模（mó）擬了一（yī）下劉歆的計算過程，推算出劉歆所用的（de）圓周率是162方寸÷(7.166寸)²=3.1547。祖（zǔ）衝之推算出劉歆（xīn）的圓周率（lǜ）後（hòu），十分讚賞，因為在劉歆（xīn）所處的西漢末年，最著名的數學書《周髀算經》裏說的（de）是“徑一（yī）周三”。就是說，圓周是直徑的三倍，如果直徑是一尺，圓（yuán）周率（lǜ）就是（shì）三尺。圓（yuán）周（zhōu）率是3，而劉歆所用的圓周率卻是（shì）3.1547，比起“徑一周三”的算法進步（bù）很多。這提起了祖衝之更大的興趣。祖衝之知道，劉徽在劉歆之後已采用（yòng）了割圓術計算出圓周率是3.14。劉徽這種方法是有正確的理論作指導的，對這一點祖衝之深信不疑，同時也是心悅誠服的。但是，劉徽隻取了小數點後兩位數，把後麵幾位數舍棄了。祖衝之覺得，如果不算出更精確的圓周率，也就（jiù）沒有辦法更進一步（bù）精確地校核嘉量的計算容（róng）積。於是決心按照這一方法繼續計算下去。為此（cǐ）祖衝之把（bǎ）自己的小書房重新翻修，把地板刨得（dé）十分光滑。祖衝之的兒子祖暅(gèng)看到後，不解地問道:“您這是（shì）要（yào）做什（shí）麽呀?”祖衝之回答說:“我想計算出比劉徽更精確的圓周率。”祖暅在父親的影響下，也對數學很感興（xìng）趣，十分高興（xìng）地說:“我來做您的幫手吧。”祖（zǔ）衝之高興地點頭（tóu）答應了。祖衝之（zhī）和兒子一起，在書（shū）房的（de）地上畫了一個直徑為一丈的（de）大圓，開始了艱苦的計算。劉徽算到96邊形就停止了，而祖衝之則算到12288邊形才停下來。為此祖（zǔ）衝之父子（zǐ）幾乎是廢寢忘食、夜（yè）以繼日，無數次耗盡燈油。終於得出比劉徽更精確（què）的圓周率，即（jí）:如果直徑是1，圓周大於（yú）3.1415926，小於3.1415927。這個結論，用現代數學符號表示（shì）:3.1415926<π<3.1415927。祖衝之當時也（yě）並不知道，他已成為全世（shì）界最早把（bǎ）圓周（zhōu）率精確地計算到小數點後七位數的第一人。祖衝之（zhī）求得了這（zhè）個精確的圓周率後，再去（qù）校驗嘉量上的刻銘，終於發現劉歆的計算還是（shì）不夠精確，他（tā）指出:嘉量圓麵積（jī）設計162平方（fāng）寸，按圓周率是3.1415926計算，半徑是7.180965寸，直徑是14.36193寸有餘，這樣，庣旁就不是（shì）銘文所說的九厘五毫，而（ér）正確的庣旁（páng）應該是（shì）一分九（jiǔ）毫有餘，劉歆庣旁比理論值少了一厘四毫有餘。他（tā）再用這個數字和自己求得的圓周率去（qù）計（jì）算嘉量（liàng）的容積，果然得（dé）到1620立（lì）方（fāng）寸。劉歆設計（jì）製造了這樣一件量器，甚至（zhì）影響到數學上重大成果的取（qǔ）得，這是（shì）連他自己也不會想到的。曆代對新莽銅嘉量都給予了極大的關注，唐（táng）宋時盡管仍（réng）不斷有學者對它做過討論（lùn）、研究（jiū），但都懷疑實物是否還存在？元、明兩代四（sì）百年間，也未見有新莽銅嘉量（liàng）的下落。到了清朝乾隆初年，新莽銅嘉量被（bèi）發現藏於內府，乾（qián）隆皇帝對它給（gěi）予了極大的關注，並（bìng）參照（zhào）新莽銅嘉量設計製（zhì）造了三圓一方乾隆（lóng）嘉量，把方、圓兩件分別（bié）陳設在（zài）乾清宮和太和殿前亭屋內，以象（xiàng）征清廷的法度與至高無（wú）上的權力。1924年，紫禁城被改造籌建為（wéi）故宮博物院，在清點文物時發現了這件珍品，再次引起學術界的關注，隨（suí）後馬（mǎ）衡、王國（guó）維、劉複等相（xiàng）繼對它作了（le）研究、考證，對這件曠世瑰寶在曆史、科學技術、數（shù）學、度量衡等方（fāng）麵所起的作用給予了高度評價。劉複受當時任博物院院長馬衡先生的重托，對嘉量作了（le）十分精細的測量，並寫了《新嘉量之校測與推算》一文（wén），詳（xiáng）細記（jì）述了測量方法（fǎ）及推算經過（guò），最後求（qiú）得新莽（mǎng）時一尺（chǐ）長23.1厘米、一升容200毫升、一斤重226.7克。新莽銅嘉量在其（qí）後的兩（liǎng）千（qiān）年，不斷引（yǐn）起後世如此多的關注，在世界度量衡史上也（yě）是絕無僅有（yǒu）的。如今，這件國之瑰寶仍保存良好，珍藏於台灣故宮博物院。