計量培訓:通用計量術語知識講座
中（zhōng）國計（jì）量科學研究院（yuàn）  施昌彥

一（yī）、測量誤差和相對誤差

　　1.[測量]誤差（chà）是指“測量（liàng）結果減（jiǎn）去被測量的真值”(5.16條)。
　　這（zhè）個定義從20世紀70年代以來沒有發生（shēng）過（guò）變化，以公式表示為:測量誤差=測量結果-真值。測量結果（guǒ）是（shì）由測量所得到的賦予被測量的（de）值，是客觀存（cún）在的量的實（shí）驗表現（xiàn），僅是對測量所得被測量之值（zhí）的近似或估計，顯（xiǎn）然它是人們認識的結果，不僅與量的本身有關，而（ér）且與測量（liàng）程序、測量儀器、測量環境以及測量人（rén）員等有關。真值是量的定義的完整體現，是與給定的特定量（liàng）的定義完全一致的值，它（tā）是（shì）通過完善（shàn）的或完美無缺的測量，才能獲得的值。所以，真值反（fǎn）映了人們（men）力求接近的理想目標或客觀真理，本質上真值是不能（néng）確定的，量子效應排除了唯一真值（zhí）的（de）存在，實際上用的是約定真值，須以測量不確定度來表征其所處的範圍。因而作為（wéi）測量結果（guǒ）與真（zhēn）值之差的測（cè）量誤差，也是無法準確得到或確切獲知的。

　　這裏應予指出（chū）的（de）是:過（guò）去人們有時會誤用誤差一詞，即通過誤差分析給（gěi）出的往往是被測量值不能確定的範圍（wéi），而不是真正的誤差值。按定義誤差與測量結果有關，即不同的測量結（jié）果有不同（tóng）的誤差，合理賦予的被測量（liàng）之值（zhí），各有其誤差而並不存（cún）在一個共同的誤差。一個測量結果的誤差，若不是正值(正誤差)就（jiù）是（shì）負值（zhí）(負（fù）誤差)，它取決於這個結果是大於還是小於真值。
　　如圖所示，被測量值為y，其真值為t，第i次測量所（suǒ）得的觀測值或測得值為y_i。由於誤差（chà）的存在使測得值與真值不能重合，設測得值呈正態分布（bù）N(μ，σ)，則（zé）分布（bù）曲（qǔ）線在數軸上（shàng）的位置(即μ值)決定了係統誤差的大（dà）小，曲（qǔ）線的形狀(按σ值)決定了隨（suí）機誤（wù）差（chà）的分布範圍[μ-kσ，μ+kσ]及其在範圍內取值的概（gài）率。由圖可見，誤差和它的概率分布（bù）密切相關，可以用概率論和數理統計的方法來恰當處理。實際上，誤差可（kě）表示為:
　　誤差=測（cè）量結果-真值=(測量結果-總體均值（zhí）)+(總（zǒng）體均值-真值)=隨機誤差+係統（tǒng）誤差
    

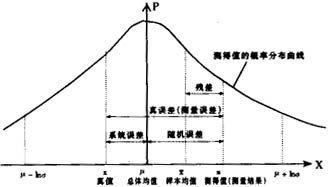
　　因此，任意一個誤（wù）差Δ_i均可分解為係統（tǒng）誤差ε_i和隨機誤差δ_i的代數和(見5.19和（hé）5.20條)，即可用下式表示為Δ_i=ε_i+δ_i。實際上，測（cè）量（liàng）結果的誤差往往是（shì）由若幹個分量（liàng）組成的，這些分量按（àn）其特性均可分為隨機誤差與（yǔ）係統誤差兩大類，而（ér）且無例外地取各分量的代數和，換言之，測量誤（wù）差（chà）的合成隻用“代（dài）數和”方式。
　　不要把誤差與不確定度混為一談。測量不確定度表明賦予被測量之值的分散（sàn）性，它（tā）與（yǔ）人們對被測量的認識程度有關，是通過分析和評定得到的一個區間。測量誤（wù）差（chà）則是表明測量結果偏離真值的差值，它客觀存在但人們無法準確得到 。例如（rú）:測量結果可能非常接近於真值(即（jí）誤（wù）差很小)，但由於認識（shí）不足，人（rén）們賦予的值卻落在一個較大區間內(即（jí）測量不確定（dìng）度（dù）較大)；也可能實際上測量誤差較大，但（dàn）由於分析估計不足，使給出的不確定度偏小。國際上開始研製成功銫原子頻率標準（zhǔn）時，經分析其測量不確定度達到10^-15量（liàng）級，運行一段時間後，發現有（yǒu）一項重要因素不可忽視，經（jīng）再次分析（xī）和評定，不確定度擴大到（dào）10^-14量級，這說明人們的認識（shí）提高（gāo）了。因此，在評定測量（liàng）不確定度（dù）時應充分考慮各種影響因素，並對不確定（dìng）度（dù）的評定進行（háng）必要的（de）驗證。
　　當有必要與相（xiàng）對誤差相區別時，此術語有時稱為測量的絕對誤差。注意不要與誤差的絕（jué）對值（zhí）相混淆，後者為誤差的模。

　　2.相對誤差是指“測（cè）量誤（wù）差除以被測量的（de）真（zhēn）值”(5.18條)。
　　設測量結果（guǒ）y減去被測量（liàng）約定真值t，所得的（de）誤差或絕對誤差為Δ。按定義將絕對誤差Δ除以約定真值t，即（jí）可求得相對誤差為δ=Δ/t×100%=(y-t)/t×100%。所以，相對誤差表示絕對誤差所（suǒ）占約定真值的百分比，它也可用數量級來表示所占的份額或（huò）比例，即表（biǎo）示（shì）為
　　δ=[(y/t-1)×10ⁿ]×10^-n
　　當被測量（liàng）的大小相（xiàng）近時，通常用絕對（duì）誤差進行測量水平的比較。當被測量值相差較大時，用相對誤差才能進（jìn）行有效的（de）比較。例如:測量標稱值為（wéi）10.2mm的（de）甲棒（bàng）長度時得（dé）到實際值為10.0mm，其示值誤差Δ=0.2mm；而測量標稱值為100.2mm的乙棒長度時得到實際值（zhí）為100.0mm，其示值誤差Δ′=0.2mm。它們的（de）絕對誤差雖然相同，但乙棒的（de）長度是甲棒的10倍左右，顯然要比較或反映兩者（zhě）不同的測量水平，還須用相對誤差或誤差率的概念。即δ=0.2/10.0=2%，而δ′=0.2/100.0=0.2%，所（suǒ）以乙棒比甲棒準確，或者用數量級表（biǎo）示為δ=2×10^-2，δ′=2×10^-3，從而也反映出後者的測量水平高於前者一個數量級。

　　另外，在某些場合下（xià）應用相對誤差還有方便之（zhī）處。例如:已知質量（liàng）流量計的相對誤差為δ，用它測定（dìng）流量為Q(kg/s)的某管道所通過（guò）的流體質（zhì）量及（jí）其誤差（chà）。經過時間T(s)後流（liú）過的質量為QT(kg)，故其絕對誤差為QδT(kg)。所以，質量的相（xiàng）對誤（wù）差仍為QδT/(QT)=δ，而與時間T無關。
　　還應指出的（de）是（shì）:絕對誤差與被測量的量（liàng）綱相同，而相對誤差是量綱一的量或無量綱量。 

   [page_break]

　　二、隨（suí）機誤差和係統誤差

　　1.隨機誤差是（shì）指“測量結果與在重複性條件下，對同一被測量進行無限多次（cì）測量所得（dé）結果的平（píng）均值之差”(5.19條)。
　　這是（shì）1993年由BIPM、IEC、ISO、OIML等國際組織做了原則修改後的（de）新定義。它表明（míng）測量結果是真值、係統誤差與隨機誤差這三者的代數（shù）和；而（ér）測量結果與無限多次測量所得結果的平均值(即總（zǒng）體均值（zhí）)差，則（zé）是這一測量（liàng）結果的隨機誤差分量。隨機誤差（chà）等於誤差減去係統誤差。1993年前，隨機誤差被定義為在同一量的多次測（cè）量過程中（zhōng），以不可預知方式變化的測量誤差（chà）的分量。
　　老定義中（zhōng）這個以不可預知方式變化的（de）分（fèn）量，是（shì）指相同條件下多次測量時誤差的絕對值（zhí）和符號變化不（bú）定的分量，它時大時小、時正時負、不可預定。例如:天平的（de）變動性、測微儀的示值變（biàn）化（huà）等，都是隨機誤差分量的反映。事實上，多次測量時的條件不可能絕對（duì）地完全相同，多（duō）種因素的（de）起伏變化或微小差（chà）異綜合在一起，共（gòng）同影響而致使每個（gè）測得值的（de）誤差（chà）以不可（kě）預定的方式變化。現在，隨機誤差是按其本質（zhì）進行定義的，但可能確定的隻是其估計值，因為測量隻能進行有限次（cì）數，重複測（cè）量也（yě）是在“重複性條件”下（xià）進行的(見5.6條)。就單個隨機（jī）誤差估計（jì）值而言，它沒有確定的規（guī）律；但就整體而言，卻服從一定的統計（jì）規律，故可用統計方（fāng）法估計其界限或（huò）它對測量結果的影（yǐng）響。

　　隨機誤差大抵（dǐ）來源於影（yǐng）響量的變（biàn）化，這種變化在時間上和空間（jiān）上（shàng）是（shì）不可（kě）預知的或隨機（jī）的（de），它會引起被測量重複觀測（cè）值（zhí）的變化，故稱之為“隨機效（xiào）應”。可以認為正是這種隨機效應導致了重複觀測中的分散性，我們用統計方法得到的實（shí）驗標準[偏]差是分散性，確切地說是來源於測量過（guò）程中的隨機效應，而並非來（lái）源於測量結果（guǒ）中的隨機誤（wù）差分量。
　　隨機誤差（chà）的統計規律性，主要可歸納為對稱性、有（yǒu）界性和單（dān）峰性（xìng）三條:

　　1.對稱性是指絕對值相等而符號相反的誤差（chà），出現的（de）次數大致相等，也即測得值是以它們的算術平均值為中心而對稱分（fèn）布的。由於所有誤差的代數和趨近於零，故隨機誤差又具有抵償性，這個統計特性（xìng）是最為本質的；換言（yán）之，凡具有抵償性的（de）誤差，原則上均可按隨機誤差（chà）處理。
　　2.有界性（xìng）是指測得值誤差的絕對值不會超過一（yī）定的（de）界限，也即不（bú）會出現絕（jué）對（duì）值很大（dà）的誤差。
　　3.單峰性是指絕對值小的誤差比絕對值大的誤差數目多，也即測（cè）得值是以它們的算術平均值為中心而相對集中地分布的。

　　2.係（xì）統誤差是指“在重複性條件下（xià），對同一被測量進行無限多次測（cè）量所得結果的平均值與被測量的（de）真值之差”(5.20條)。
　　由於隻能進行有限次數（shù）的重複測量，真值也隻能用約定真值代替，因此如真值一樣，係統誤差及其原因不能完全獲知可能確定的係統誤差，隻是其估計值，並具有一定的不確定度。這個不確定度也就是修正值的（de）不確定度，它與其他來源的不確定度分量一樣貢（gòng）獻給了合（hé）成標（biāo）準不確定度。值得指出的是:不宜按過去（qù）的說法把係統誤差（chà）分為已定係統誤（wù）差和（hé）未（wèi）定係（xì）統誤差，也不宜說未定（dìng）係統誤差按隨機誤差處理。因為（wéi）這裏所謂的未定係統誤差，其實並不是誤差分量而是不確定度（dù）；而且所謂按隨機誤差處（chù）理，其概念也是不容易說得清楚的。
　　係統誤差大抵來源於影響量，它（tā）對測（cè）量結果（guǒ）的影（yǐng）響若已識別並可定量表述，則（zé）稱（chēng）之為“係統效應”(systematic effect)。該效應（yīng）的大小若是顯著的，則可通（tōng）過估計的（de）修正值予以補償。例如:高阻抗（kàng）電阻器的電位（wèi）差(被測量)是用電壓表測量的，為減（jiǎn）少電壓表負（fù）載效應給測量結果帶來的“係統效應”，應對該表（biǎo）的有限阻（zǔ）抗進行修正。但是，用以估計修正值的電壓表阻抗與電阻器阻抗(它們均由其（qí）它測量獲得)，本身就（jiù）是不確定的。這些不確定度可用於評定電位差的測量不確定度分量，它們來源（yuán）於修正，從（cóng）而來源於（yú）電壓表有（yǒu）限阻抗的係統效（xiào）應。另外，為了盡可能消除係統誤差（chà），測量器具須經常地用計量標準或（huò）標準物質進行調整或校準；但是同時（shí）須考慮的是:這些標（biāo）準（zhǔn）自身仍帶著不確定度（dù）。

　　至於誤差限、最大允許（xǔ）誤差、可能（néng）誤差、引用誤差等術語，它們前麵帶有正（zhèng）負(±)號，因而是一種可能誤差的分散區間，並不是某個測（cè）量結果的誤差。對於測量（liàng）儀器而言，其示值的係統誤差稱為測量儀器的“偏移”(bias)，通常用適當次數重複測量示值誤差的均值來估計。
　　過去所謂的“誤差傳播定律”，所傳播的其實並不是（shì）誤差，而是不（bú）確定度（dù）。現（xiàn）在已改稱（chēng）為“不確定度傳播定（dìng）律”。還要指出（chū）的是:誤差一（yī）詞應按其定義使用（yòng），不宜用它來定量表明測量結果的可靠程度。
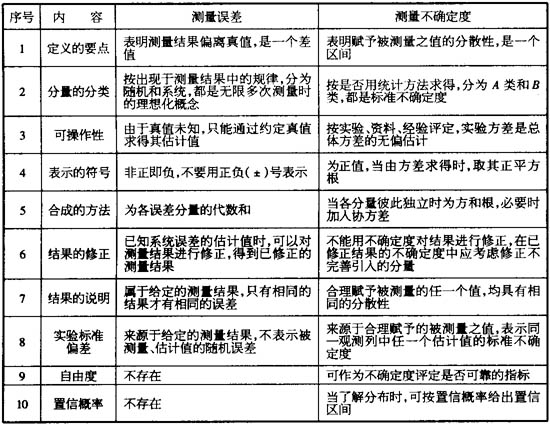
　　歸納一下《通用計量術（shù）語及定義（yì）》5.16～5.20條以及5.9～5.14條的要點，可將測量誤差與測量不確定度之間存在的主要區別用下（xià）表簡示。
    

　　三、修正（zhèng）值、修正因子及偏差

　　1.修正值是（shì）指“用代數方法與未修正測量結果相加，以補償其係統誤差的值”(5.21條)。
　　含有誤差（chà）的測量結果，加上（shàng）修正值後就可能（néng）補償或減少誤差的影響。由於係統（tǒng）誤差不能完全獲知，因此這種補償並不完全。修正（zhèng）值等於負的係統誤差，這就是說加（jiā）上某個修正值，就像扣掉某個係統誤差，其效果是一樣的，隻是人們考慮問題的出發點不同而已:
　　真值=測量結果+修正值（zhí）=測量結果-誤差
　　在量值溯源和量值傳遞中，常常采用這種加修正值的直觀（guān）的辦法。用（yòng）高一個等級的計量標準來校準（zhǔn）或檢定測（cè）量（liàng）儀器，其主要內容之一就是要獲得準確的修正值。例如:用頻率為fs的標準振蕩器作為信號源，測得某台送檢的頻率計（jì）的示值為f，則示值誤（wù）差Δ為（wéi）f-fs。所以，在今後使用這台頻率計時應扣掉這個（gè）誤差，即加上修正值(-Δ)，可得f+(-Δ)，這樣就與fs一（yī）致了（le）。換言之，係統誤差可以（yǐ）用適當的修正值來估計並予以（yǐ）補償。但應（yīng）強調指出:由於（yú）係（xì）統誤差不能完全獲知，因此這（zhè）種補償是不完全的，也即修正值本身就含有不確定度。當測量結果以代數（shù）和方式與修正值相加之後，其係統誤差之模會比修正前的要（yào）小，但不可能為零，也（yě）即修正（zhèng）值隻能對係統誤（wù）差進行有（yǒu）限程度的補償。

　　2.修正因子是指“為補償係統（tǒng）誤差而與未修正測量結（jié）果相乘的數字因子”(5.22條)。
　　含有係統誤差的測量結果，乘（chéng）以修正因數後就可以補（bǔ）償或減少誤差的影響。比方由於等（děng）臂（bì）天（tiān）平的不等臂誤差，不等臂天平的臂比誤差（chà），線性標尺分度時的倍數誤差，以及測量電橋臂的不等稱誤差所帶來的測（cè）量結果中的係統誤差，均可以通過乘一個修正因數得以補償。但是，由於係統誤差並不能完全獲知，因而這種補償是不（bú）完全的，也即修正（zhèng）因數本身（shēn）仍含有不確（què）定度。
　　通過修正因子或修正值已進（jìn）行了修（xiū）正的測量結果，即使具有較大的不確（què）定度，但可能仍（réng）然十分接近被測（cè）量的（de）真值(即誤差（chà）甚小（xiǎo）)，因此，不應把測量不確定度與已修正測量結果的誤差相混淆。

　　3.偏差是指“一個值（zhí）減去其參考值”(5.17條)。
　　以測（cè）量（liàng）儀器（qì）的（de）偏差為例（lì），它是（shì）從零件加工的“尺寸偏差”的概念引伸過來的。尺（chǐ）寸偏（piān）差是加（jiā）工所得的某一實際尺寸，與（yǔ）其要求的參考尺寸或標稱尺（chǐ）寸之差。相對於實際尺寸來說，由於加工過程中諸多因素的影響，它偏離了要求的或應有的參（cān）考尺寸，於（yú）是產生了尺寸偏差，即
　　尺寸偏差（chà）=實際尺寸-應有參考尺寸
　　對於量具也有類似情況（kuàng）。例如:用戶需要一個準確值（zhí）為1kg的砝（fǎ）碼，並將此應有的值標示在砝碼上；工廠加工時由（yóu）於諸多因素的影響，所得的實際（jì）值（zhí）為1.002kg，此時的偏（piān）差（chà）為+0.002kg。顯然（rán），如果（guǒ）按照標稱值1kg來使用，砝碼就有-0.002kg的示（shì）值誤（wù）差；而如果在標稱值上加一個修（xiū）正（zhèng）值+0.002kg後再（zài）用（yòng），則這塊砝碼（mǎ）就顯得沒有誤（wù）差了。這裏的示值誤差和修正值，都是相對於標稱值而言的。現在從另一個角度來看，這塊砝碼（mǎ）之所以具有-0.002kg的示值誤差，是（shì）因為加工發生偏差，偏大（dà）了0.002kg，從而使加工出來的實際值(1.002kg)偏離（lí）了標稱值(1kg)。為了（le）描述這個差異，引入“偏差”這個概（gài）念就是很自然的事，即
　　偏差（chà）=實際值（zhí）-標稱值=1.002kg-1.000kg=0.002kg
　　在（zài）此可見（jiàn），定義（yì）中的偏差與修正值相等，或與誤差等值而反向。應強調指出的是:偏（piān）差（chà）相（xiàng）對於實際值而言，修正值與誤差則相（xiàng）對於標稱（chēng）值（zhí）而言，它們所指的對象不同。所以在分析時，首先要分清所研究的對象是什麽。還要提及的是:上述尺寸偏差也稱實際偏差或簡稱偏（piān）差，而常見的概（gài）念還有“上偏差”(最大極限（xiàn）尺寸與應有參考尺寸之差)及“下偏差”(最小極限尺寸與應有參考尺寸之差)，它們統稱為“極限偏差”。由代表上、下偏差的兩條直線所確定的區域，即（jí）限製尺寸變動量的區域，通稱為尺寸公差帶。