計量培訓：測量不確定度表述講（jiǎng）座
湖北財經學（xué）院（yuàn）　李興仁（rén）

　　4.1  什麽叫統計方法？
　　測量不確（què）定度的A類評定方法定義為統計方法。所謂統計，一（yī）般來說，是（shì）指根據（jù）從總體中隨機取出的樣本（běn）中（zhōng）所（suǒ）獲得的信息來推斷關於總體性質的方法（fǎ）。
　　一個被測量的某（mǒu）種條件(重複性（xìng）條（tiáo）件或複現性條件)下的任一個測量結果，可視為無限多次測量結果(總體)的一個樣本。通（tōng）過有限（xiàn）次數的測量結果(有限的隨機樣本（běn）)所獲得的信息(例如:平均值大小（xiǎo）、實（shí）驗標準（zhǔn）偏差s(y))，來推斷總體的平均值(稱之為總體均值μ或稱為該分布的期望值)以及總體標準差σ，就是一種統（tǒng）計方法。

　　4.2  什麽是期望、期望值與最佳估計？
　　在不確定度評定中，無限多次的重複性條件（jiàn）下或複現性條件（jiàn）下（xià）的測量結果的平均值以及（jí）非等精度條件下的加權平均值，均為期望值或簡稱期望。它也是總（zǒng）體的（de）均值μ，隻是理論上（shàng）存（cún）在。
　　有限次數（shù）的測量結果（guǒ）都隻是（shì）被測量的一個估計。當重複了若幹次測量，得到若幹個測量結果時，隻有它們的平均值才是最佳估計，如果存在（zài）修正值，則隻能是修正（zhèng）後的結果才是最佳估計。
　　任何一個估計及最（zuì）佳（jiā）估計值均具（jù）有不為零的不確定（dìng）度，而期望值的不（bú）確定度恒等於零。

　　4.3  什麽是概率（lǜ）？概率分布與主觀概率、先驗概率？
　　某種事件A出（chū）現的可（kě）能性大小的定量描述。例如，一個被測量（liàng）Y在一個重複性條件下的測量（liàng）結果y₁中，所包含的隨機（jī）誤差分量是正（zhèng）值還是負值，其可能性一樣大，我們說，正與負的概（gài）率各為50%。如果兩（liǎng）次測量結果y₁與y₂中所出現的隨機誤差分量（liàng）的符號相同(均為正值或均為負值)，與符號不相同(一正一負)的概率也各為50%。三個重複測量結果y₁、y₂與y₃中隨機（jī）誤差分量的符號相同（tóng），其概率就隻有25%。
　　大大小小地合理賦予被測量Y之值y_i，在其分散區間內等間隔地分成若幹(例如15個)小的區間，則（zé）y_i分別落在這些小區間中的數目多少，表明了落在這個區間的概率大小，這樣，如以縱坐標表示概率，則形成了一個概率分布曲線。下圖（tú）就是一個近（jìn）似正（zhèng）態（tài）的分布（bù）曲線，Δδ_i為每個小間（jiān）隔。
    

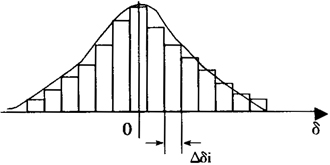
　　曲（qǔ）線表（biǎo）明了被測量可能值在多大時出現的概率有多大，同時，也可通過曲線估計出95%或99%的（de）概率（lǜ）出現在哪個區間，即所謂置信區間(參閱3.7)。如要確定概率分布曲線，往往需要有（yǒu）100～200次的重複測量結果。所謂先驗概率又稱主觀概率，則是根據（jù）觀測者的實踐經驗，對某種事件出現的概率所作出的估計。
　　常見（jiàn）的用於不確定度評（píng）定的、較為規律的概率分布曲線有:矩形分（fèn）布(又稱（chēng）均勻分布)、三角分布、梯形分布、兩點分布等（děng）。其中（zhōng）以正態分布最為常見。例如:三個以上觀測值的平均值作為被測量的結果時，這種測（cè）量結果的分（fèn）布即（jí）為（wéi）正態分布。

　　4.4  異常值指什麽？
　　由於測量條件或測量設（shè）備的（de）某種（zhǒng）偶然性變化，導致測量已（yǐ）不處於統計控製狀態；或者（zhě）由於觀測、計算、記錄中的失誤，導致某測（cè）量結果明顯偏離其所屬樣本的其餘觀測值，這樣的（de）值稱為異常值，過（guò）去，我（wǒ）們說結果中含（hán）有粗大誤差。在不確定度評定中，這樣的值是不應進入計（jì）算（suàn）而應剔除的。但（dàn）必須持慎重態度，必須按有關規則進行（háng）。特別是當觀測結果較少(例如4次)的情況下，憑4個觀測（cè）值來判（pàn）定其中某一次是異常值往往會作出錯誤（wù）結（jié）論。一般應再多重複若幹次，有了（le）例如7～8次以上的值後，再判斷哪一次的（de）結果是否為異（yì）常值。國家標（biāo）準GB4883—1985《正（zhèng）態樣本異常值的（de）判斷（duàn）和處理》可作為依據。

　　4.5  什麽叫（jiào）數學（xué）模型？
　　用數學語言給出的物理量之間或數值之間的關係式。測量的數學模型指得到被（bèi）測量Y的數學計（jì）算式。因此，同一（yī）個被測量按所選擇的測量方（fāng）法不同而有（yǒu）不同的數學模型。例如要測量一個球體（tǐ）的密度ρ，當我們選用（yòng）天平、砝碼以及已知密度ρ₀的（de）液體（tǐ），用兩次（cì）稱重(空（kōng）氣（qì）中的稱重與（yǔ）浸（jìn）入液體中的稱重)的方法得出時，
　　ρ=m/(m-m′)·ρ₀
　　式（shì）中m為在空氣中稱出的質量，m′為在浸入液體中稱（chēng）出的質量。但是，當我們（men）采用測量球體體積V的方法時，就有了另外的數學（xué）模式:
　　ρ=m/V
　　如果考慮了某種（zhǒng）修（xiū）正的計算，相（xiàng）應地，數學模型會有（yǒu）一定程度的複雜化（huà）。
　　在不確定度評定（dìng）中，我們一般把（bǎ）被測的量稱為（wéi）輸出量。上例中（zhōng）的ρ就是。把（bǎ）與ρ有函數關係的（de）、通常是直接用實驗測出的量，稱為輸入（rù）量，上例中的m、m′、ρ₀以及V都是。這些輸入量也可能（néng）是由若幹個（gè）量得出的，例如m可能是若幹個砝碼之和，V是通（tōng）過直徑測量並經過計算得出的，甚至（zhì）測V時還有溫度的修（xiū）正等。
　　數值（zhí）關係式也可用於被測量的模型，必須注意是給定（dìng）單位下的數值，其中包括經驗公式。
　　數學模型的一般（bān）表達（dá）式為:
　　Y=f(X₁，X₂，…，X_N)
　　式中Y為被測量(輸出量)，X_i是（shì）輸入量，小寫字母為它們的估計值有:
　　y=f(x₁，x₂，…，x_N)
　　最（zuì）簡單的模型如:Y=X。例如X是（shì）體（tǐ）溫計上的示值，而Y是體溫。如由兩個砝碼X₁與（yǔ）X₂在天平上平衡得出被測質量，則數（shù）學模型是:Y=X₁+X₂。如通過滴（dī）定管測出所消耗的（de）溶液體積V，則滴定管上的兩（liǎng）次讀數(滴定的開始與終了)X₁與（yǔ）X₂同V之間的關係就是:V=X₁-X₂。如果用一個標準量塊的中心長度l_s與被檢量塊中心長度l相（xiàng）比較的方（fāng）法，用（yòng）它們之間的差d來得（dé）出l時，數學模型隻是l=l_s+d；但如果考慮兩量塊間的溫度差δθ、溫度θ以及線膨脹（zhàng）係數差（chà）δα、線膨脹係（xì）數α的（de）修（xiū）正時，就成了:
　　l=l_s+d-l_s[δα·θ+α·δθ]。
　　必須注意，數學模型中不能進入帶有正負號(±)的項。

　　4.6  線性函數與非線性函數關係在計算被測（cè）量Y的估計值時有何不同（tóng）？
　　當輸入量X₁，X₂，…，X_N與輸出量Y之（zhī）間（jiān）的函（hán）數關係是（shì）:
　　Y=a₁X₁+a₂X₂+…+a_NX_N
時，這種函數稱為（wéi）線性函數。例（lì）如通（tōng）過兩個時間（jiān）的測量（liàng）得到一個時間間隔，通過在等臂天平上的若幹個（gè）砝碼得出被（bèi）測的質（zhì）量等都屬這一（yī）類，其特點是輸入（rù）量（liàng）的各項指數均為正1或負（fù）1。上式（shì）中（zhōng）的（de）各項係數a_i既可以是（shì）正值也可（kě）以是負（fù）值。當函數關（guān）係式中輸入量相乘或除或指數不是1時，稱為非線性函數關係。例如通過球體直徑的（de）測量得到球的體積，在（zài）恒定（dìng）加速度下通過時間間隔的測量得到物體所行經的（de）距離等屬於這一類。
　　例如我們（men）對兩個砝碼的質量m₁與m₂在重複性（xìng）條件下各測了10次，輸出量(我們所要求的被測量)是m=m₁+m₂。我們可以得到的10個m₁與m₂，分別相加而得出10個m，取這10個值的算術平均值作為m的最佳估計。我（wǒ）們也可用另一種方法，把10個m₁與m₂的值（zhí）先計算其算術平均值，然後把這兩個算術平均相加作為m的最佳估計。在m=這樣的線性函數時，結果相（xiàng）同。
　　但是，如果是通過球體的直徑d的測量，求體積V，例如對d測量了10次，我們可（kě）以用每一個d的結（jié）果算出10個V取其算術平均值。第二種計算方法是把10次的d先（xiān）取其算術平均值作為d的最佳估計求出體積V，由於d對V來說是非線性（xìng）函數，以第一種（zhǒng）計（jì）算方法較為優越（yuè）。

　　4.7  產生不確定度的原因（yīn）一般主要有（yǒu）哪些（xiē）？
　　一般（bān）來（lái）說，最主要的有以下幾個方麵:
　　a.檢測手段的不理想:包括所（suǒ）用的測量儀器計量性能、標準器（qì）的不確（què）定度、測量方法和測量程序帶來的不確（què）定度、測量模型不夠完（wán）整（zhěng）。
　　b.被（bèi）測量本身帶來的:包括被測量不穩定、取樣代表性不夠（gòu）、被測樣品測量前（qián）的製備不理想。
　　c.影響量的修（xiū）正:對影響量測量不可靠、修正所用物（wù）理常數（shù）不可靠、影響量（liàng）不穩定。
　　d.由於觀測人（rén）員帶來的:數據的估讀、屬於測量過程的調（diào）整、數據（jù）處理過程中的（de）修約。

　　4.8  怎樣的不確定度分量可以忽略？
　　原則上（shàng）說，其量值（zhí）的大小對合成不確定（dìng）度的影響不大者（zhě）均可忽略。例如隻有兩個不確定（dìng）度的（de）分量合成，其中的一個隻是另一個的三分之一。由於合（hé）成是取平方和開方:=1.044≈1，因此，如果（guǒ）略去了這個較小者，最後（hòu）的結果小了將近5%。應認為可（kě）以忽略。如果有4個分量，其中3個平均隻約為最大（dà）的（de）那個的三分之一，此時合成為，略去後則減小了13%，似也不算太大。如果有另（lìng）外一個分量較大，例如（rú）是最大者的二分之一（yī），那麽去掉（diào）了3個較（jiào）小的(隻有最大的三分之一)也是可以的。因此，往往忽略那些量（liàng）值較小的分量不去估算和合成，例如修正值的不確定度較（jiào）小時、修正值本身較小也不加到（dào）測（cè）量結（jié）果中時、有時測量儀器（qì）的分辨（biàn）力導致的不確定度等。

　　4.9  什麽是核查標準？
　　核查（chá）標準也是一種標準器，例如:砝碼、量塊、電阻、電池等。當我們需要經常校準某種標準（zhǔn）器時，為了檢查整（zhěng）個校準過程是否處於正常狀態，往往建立一個或一組核查標準，要求其性能較為穩定，用於周期性(例如（rú）每兩月（yuè）一次)或必要時（shí）(例如（rú）產生（shēng）了懷疑)進行核（hé）查。例（lì）如在經常校準4等量塊的實驗（yàn）室，保（bǎo）存（cún）一組(大小不（bú）同的幾個)4等量塊，每三月按常規進（jìn）行一次（cì）校準，得出其長度之值（zhí）以及校準過程中的分散性（xìng）(實驗標準偏差s)，用（yòng）於核驗校準（zhǔn）是否出現超出規定的係統性的和隨機性的誤差，用以決定校準是否處於統計控製狀態之中，可（kě）否（fǒu）繼續進行正常工作。

　　4.10  什麽是控製（zhì）圖（tú）？
　　一種標繪著根據從總體中相繼抽取的樣（yàng）本計算出的某種統計量的值，並畫有控製界（jiè）限的圖，用（yòng）於監查一個（gè）過（guò）程是否處於控製狀態之下。根據控製圖中所用的統計（jì）量（liàng）(如算術平均值、極差、實驗標準偏差、不合格率等)的不同，來確定控製圖的不同（tóng）類型（xíng）。不確定度評（píng）定中用的控製圖用於校準過程控製，通過核查標（biāo）準的定期和不定期校準，將校（xiào）準結果紀錄在圖中，每次的校準結果作為一組抽（chōu）樣，給出平均值與標準偏差兩個曲線的控製圖。一般把容（róng）許標準偏差的兩倍作為警戒極限。

　　4.11  用統計方法得到的實驗標準差是否是測量結果的隨機誤差？
　　不是，標準差是分散性的，隨機誤差的定義見3.8，本（běn）質完（wán）全不同。分散性來源於測量過（guò）程中的隨機效應，它並（bìng）非某個測量（liàng）結果的隨機誤差（chà）。